Scott's Blog

学则不固, 知则不惑

0%

机器学习：泛化误差与随机森林

发表于 更新于 分类于 阅读次数： Valine：

这一篇文章我们来了解误差，如何处理误差，以及学习随机森林的基础知识。

机器学习：泛化误差与随机森林

泛化误差 (Generalization Error)

介绍

我们知道在监督学习的线性模型中，我们数据分布符合下面的函数，即:

\[y=f(x)\]

其中，y和x是已知的，而 f 是未知的。

同时在我们的数据分布中，数据集不可能完全按照我们的函数分布，总是有些点（噪音）事覆盖在我们的函数周边：

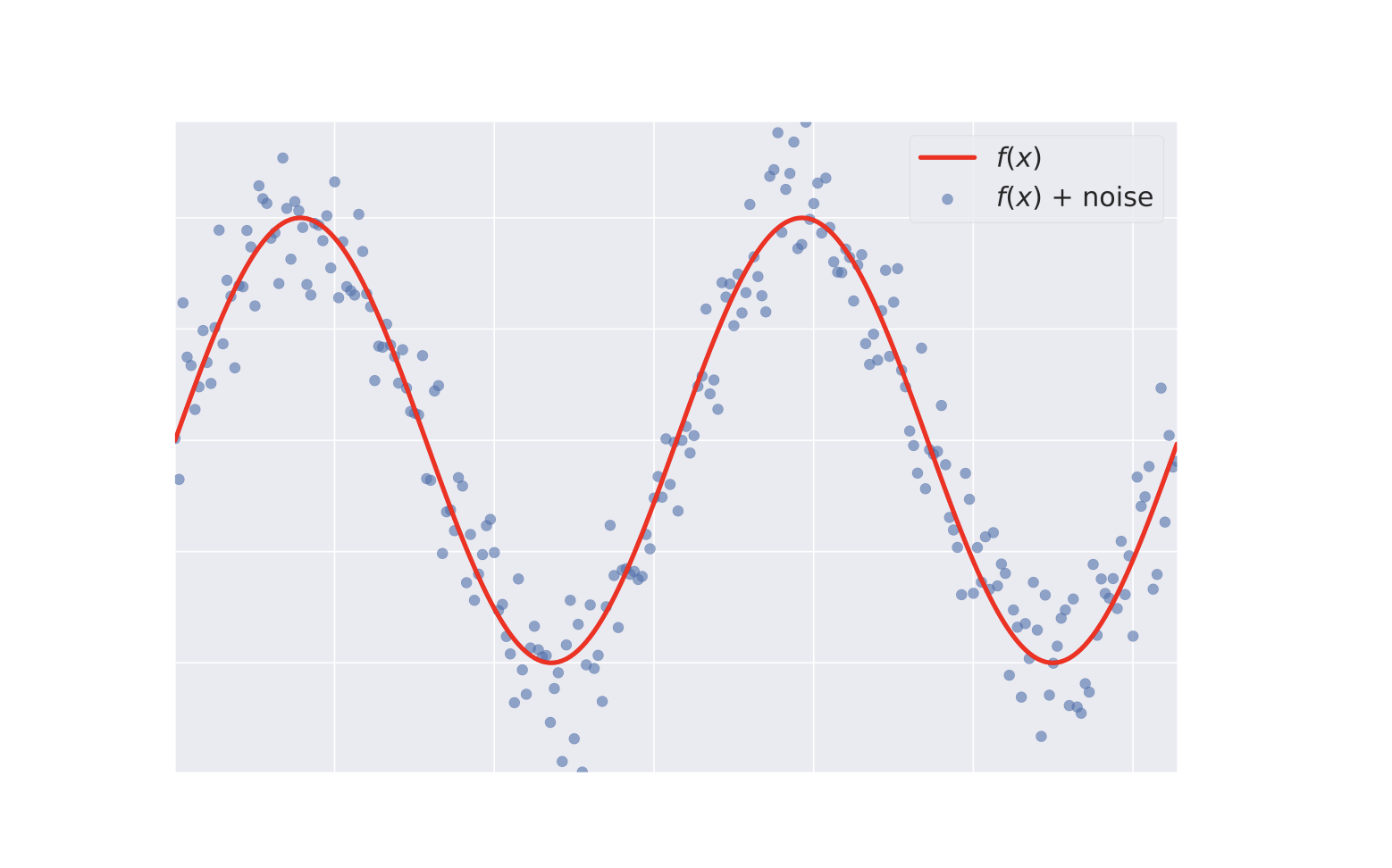
当你训练你的模型的时候，你希望这些噪音尽可能的去除，同时预测的结果尽可能少出错。

为了实现这个目标，你会遇到两个难题，即过度拟合与欠拟合。

过度拟合即我们的模型过于敏感，欠拟合即模型过于迟钝，如下面两张图图所示：

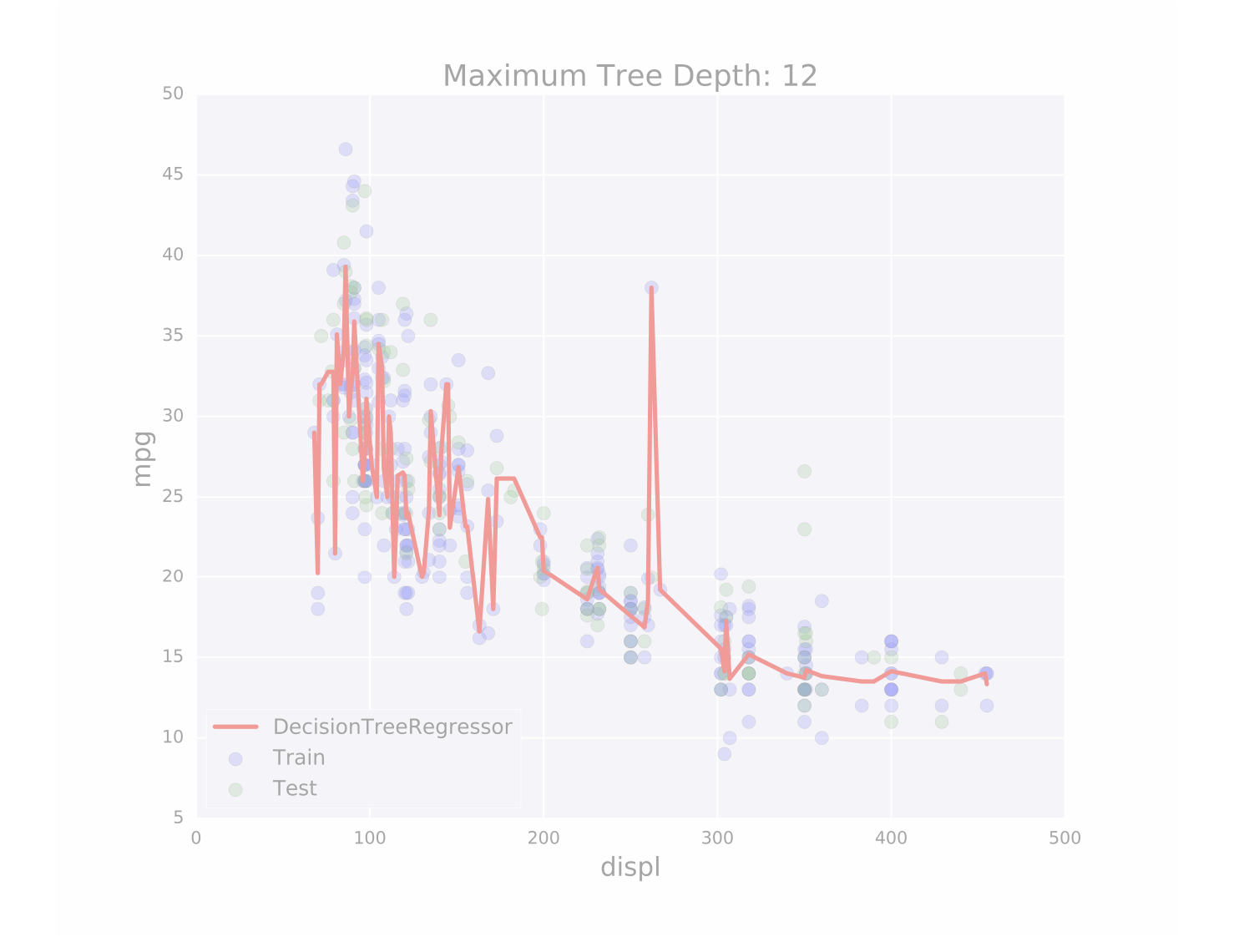
过度拟合-Overfitting
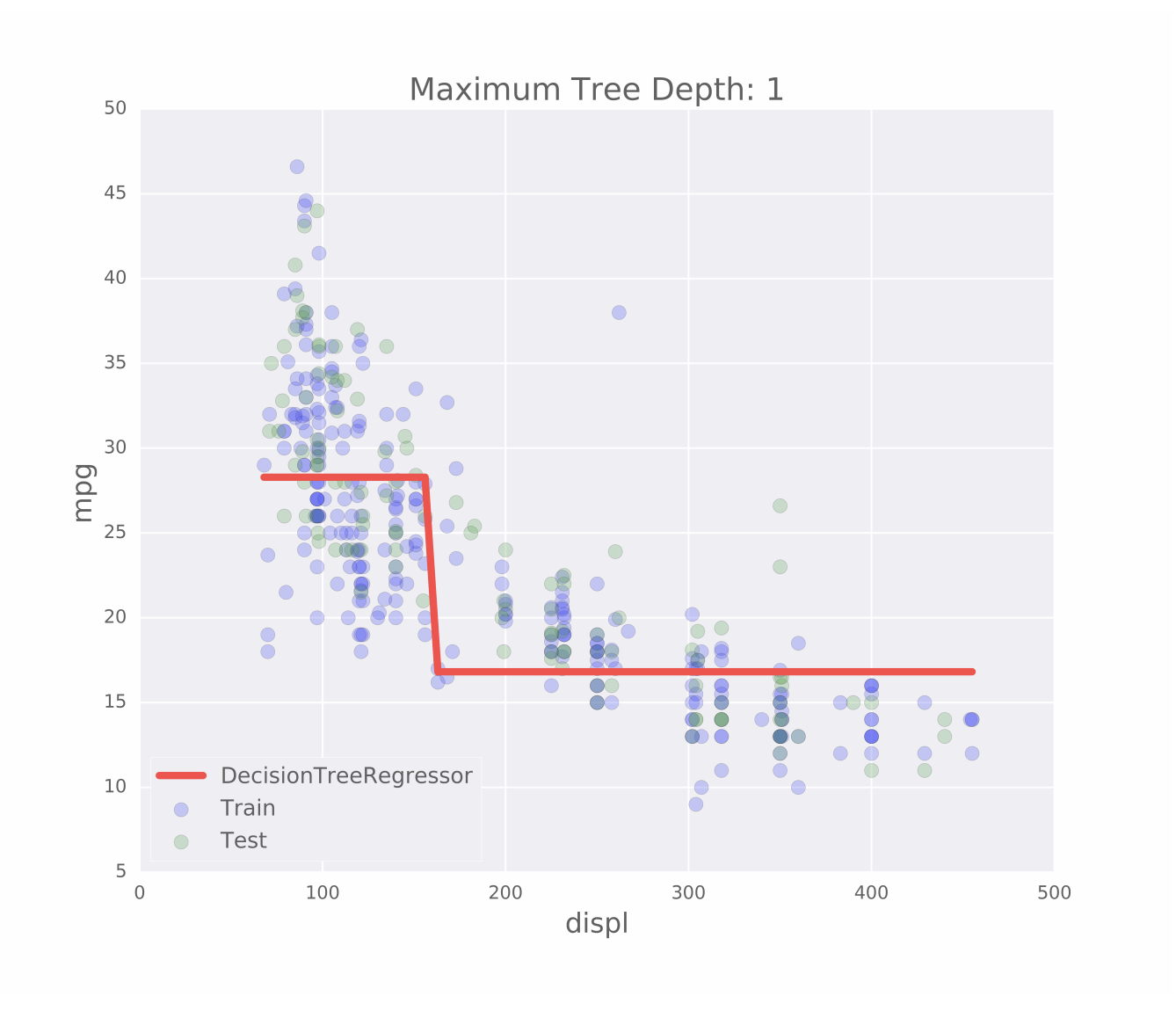
欠拟合-Underfitting

什么是泛化误差呢？这是一种衡量我们模型与数据分布之间误差，对于一个模型的泛化误差，即它对于新的数据的预测中的误差，由三个部分组成：

\[\hat{f}=bias^2+variance+irreducible\ error\]

先看第一个参数，bias。

下面是一组老鼠的体重与体长的分布数据，我们把它分割成train组与test组，我们在train组中训练我们的模型得到一条直线，可以看到数据集的分布是一条曲线，而当我们的数据集分布是一个曲线的时候，我们用一条直线是无法完整的描述数据集的分布的，无论我们怎么调整这根直线，这种情况就叫做bias:

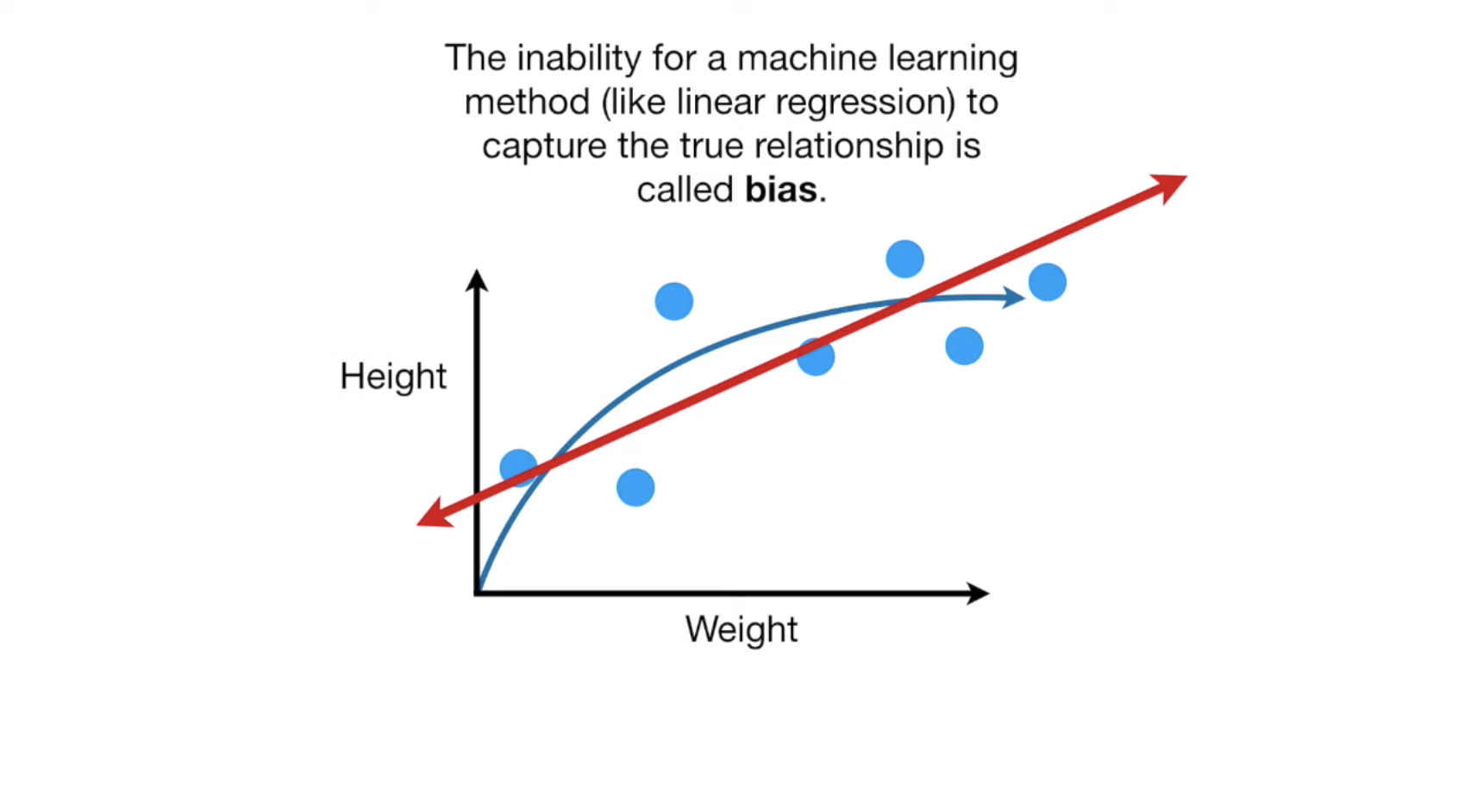
另外，我们模型也可能是生成一条曲线，而这条曲线完美的穿过了我们的train数据集：

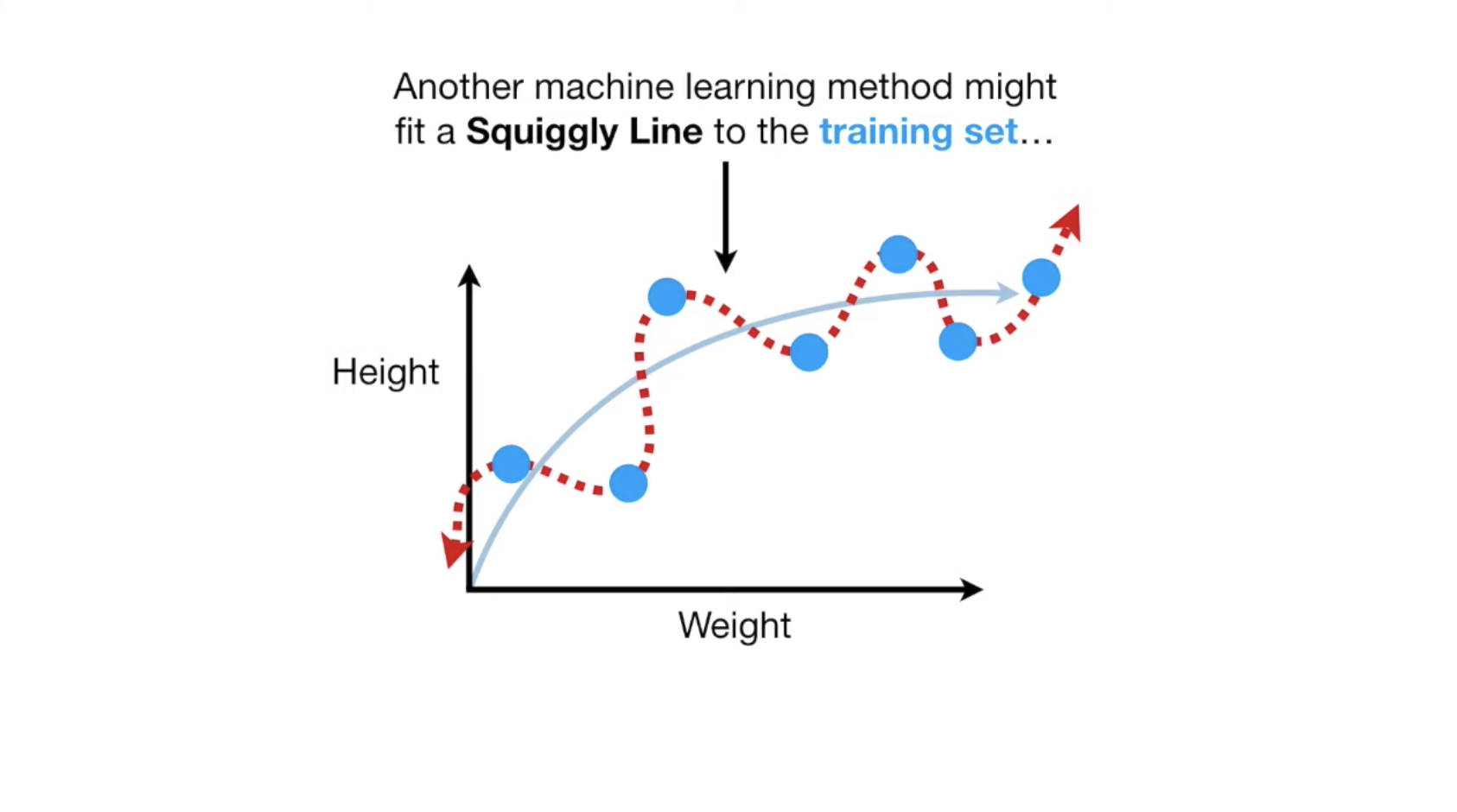
当我们用最小二乘法去衡量模型的好坏时，无疑第二个模型是最完美的，它与每个点的的距离都是0。

但是，当我们该曲线与test组的数据放到一起时，情况可能就不一样了，这就引出了variance的定义：

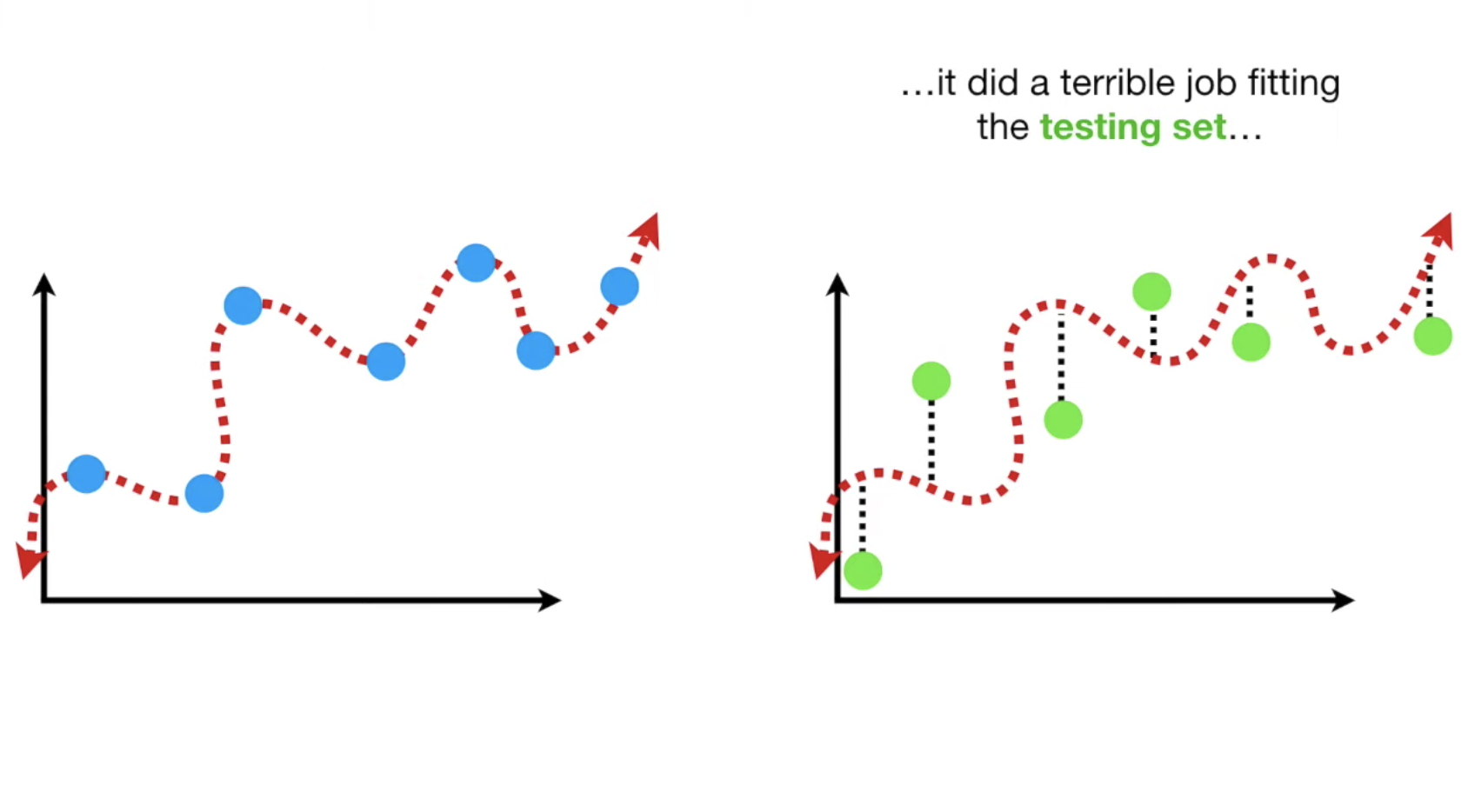
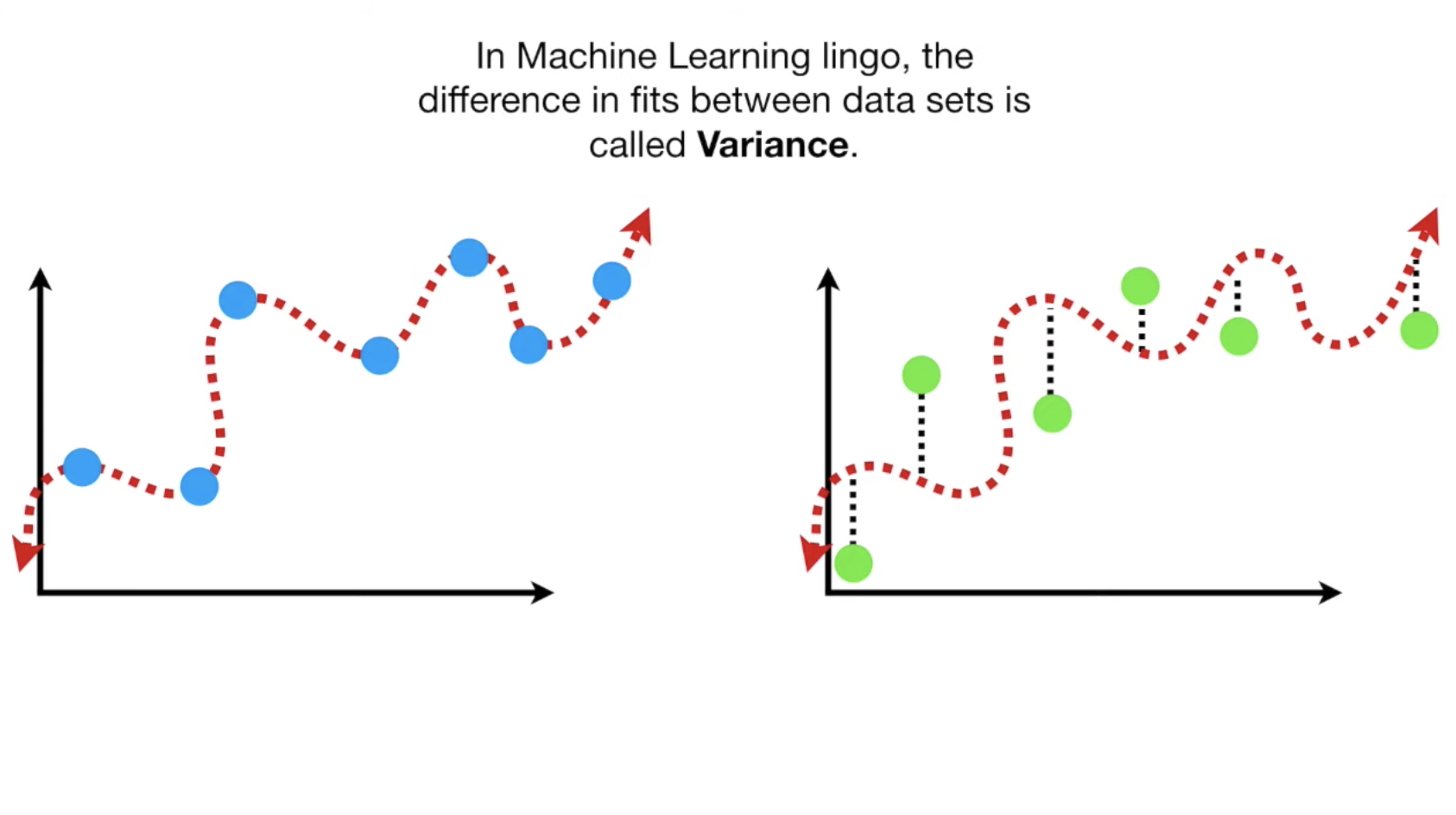
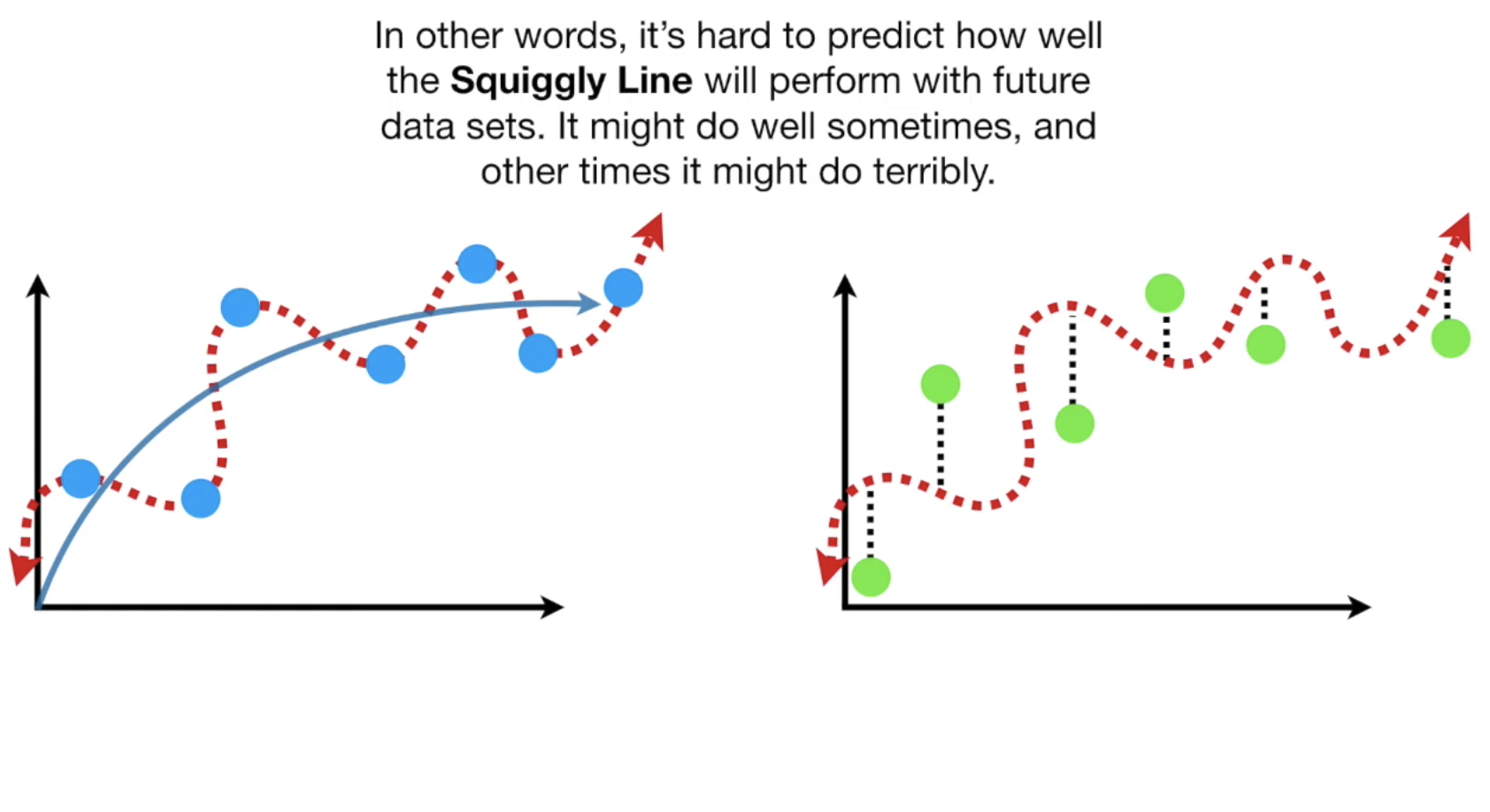
现在知道了bias以及variance，我们就知道如何去优化模型了， 我们需要均衡设置这三个参数，让他们各自都在一个最合适的位置：

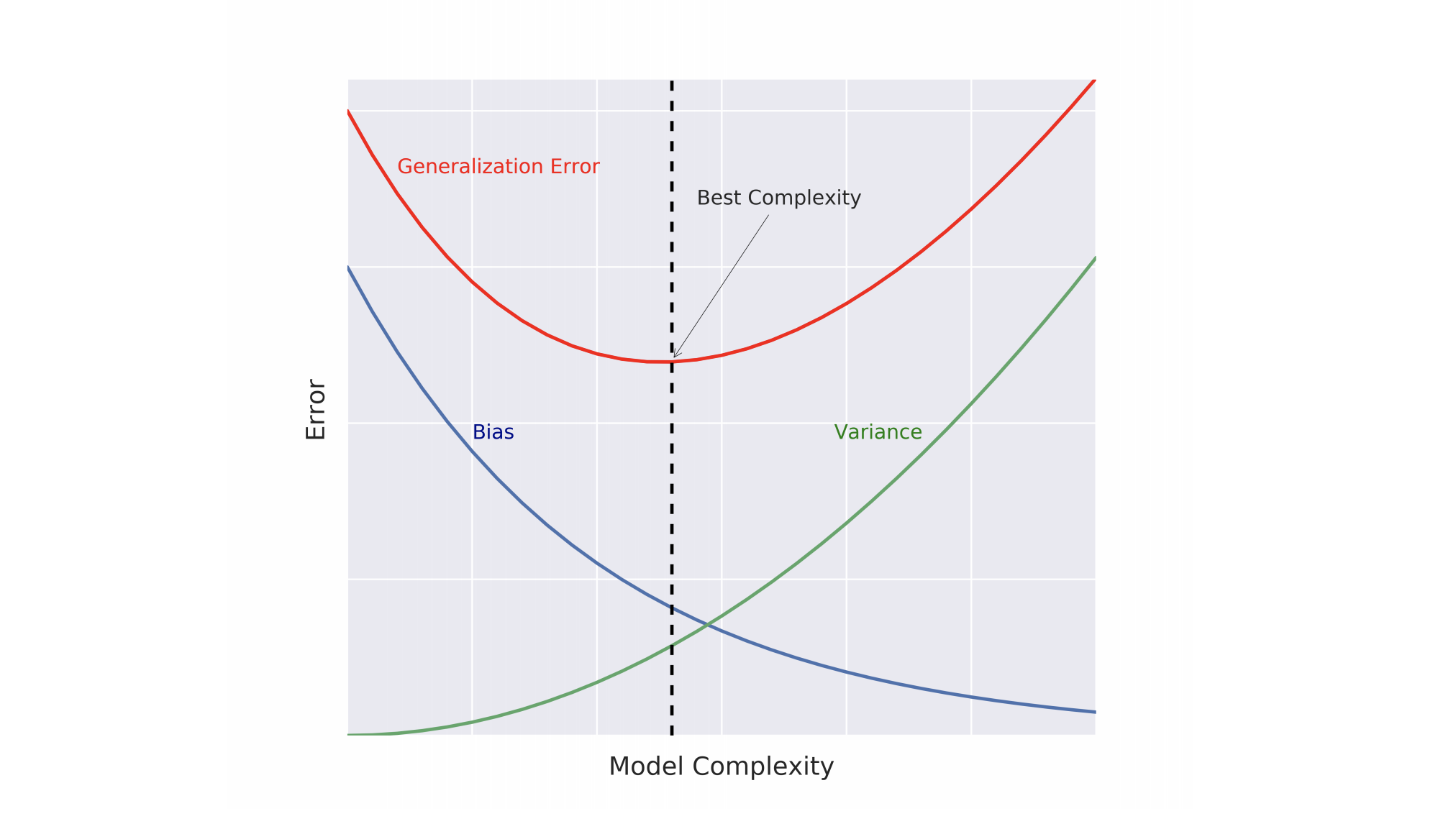
处理误差

我们尽可能的使这些误差最小，但这并不容易，首先 f 函数我们不知道，你只有一对数据，并且噪声事无法避免的。

怎么办呢？还是按照以前的方法，将数据分为train组和test组，而且我们需要使用之前介绍过的 cross-validation 技术，CV。

CV有两种：

  • K-Fold CV
  • Hold-Out CV

在这里，我们只介绍K-Fold CV, Cross-validation技术我们之前已经有过介绍，可以查看之前的文章了解详情。

在我们对数据进行fold的时，每一次fold都可以算出一次error，随后再算总的fold error平均，我们来看一个10fold的公式，其中E为每一次fold的error：

\[CV_{error}=\frac{E_1+...+E_{10}}{10}\]

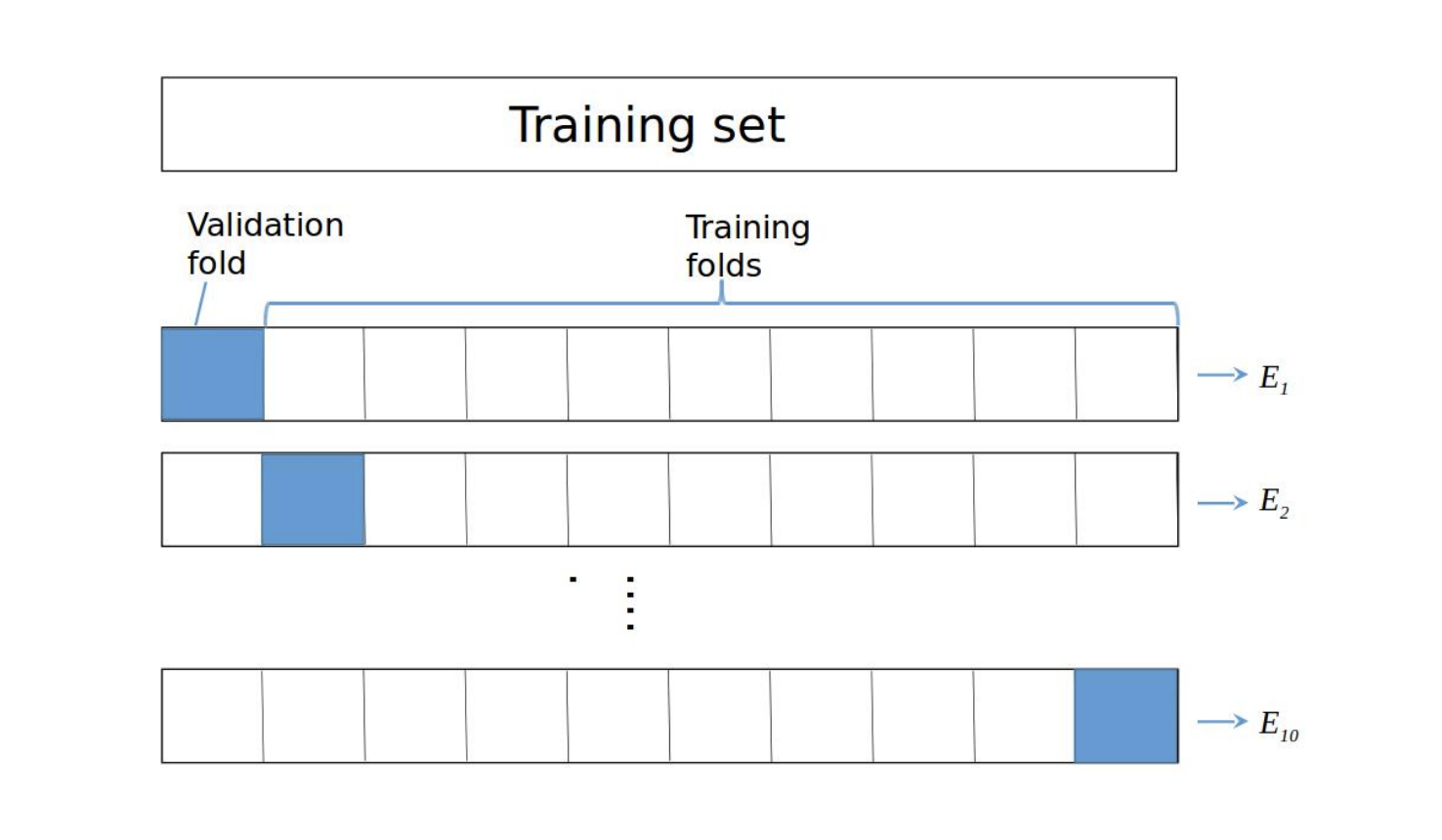
如果我们CV后的方差比train组的值要高，那就说明我们我们过度拟合了，在tree model上来看就是说我们无视了那些应该视为leaf的节点，而将其继续拆分了。如果你发现过度拟合的情况，应该降低你的模型的复杂性，比如将模型的 Max depth 降低，收集更多的数据。

如果我们的bias过高，即CV后的bias值与train组的值近似或者大于它，这意味着欠拟合，则需要增加模型的复杂性，增加模型的 Max depth,增加更多的features。

Ensemble Learning

回归一下CARTs的优点：

  1. 易于理解
  2. 容易使用
  3. 可以描述线性回归无法描述的情况
  4. 不需要标准化数据

但CARTs也有缺点，那就是容易高方差，过度拟合，不过我们可以通过 ensemble learning 解决这个问题。

简单描述一下Ensemble Learning的步骤：

  1. 用不同的模型training同一份数据
  2. 每个模型预测其自己的结果
  3. 聚合所有模型的结果
  4. 最终的预测：更可靠的数据

Ensemble prediction:

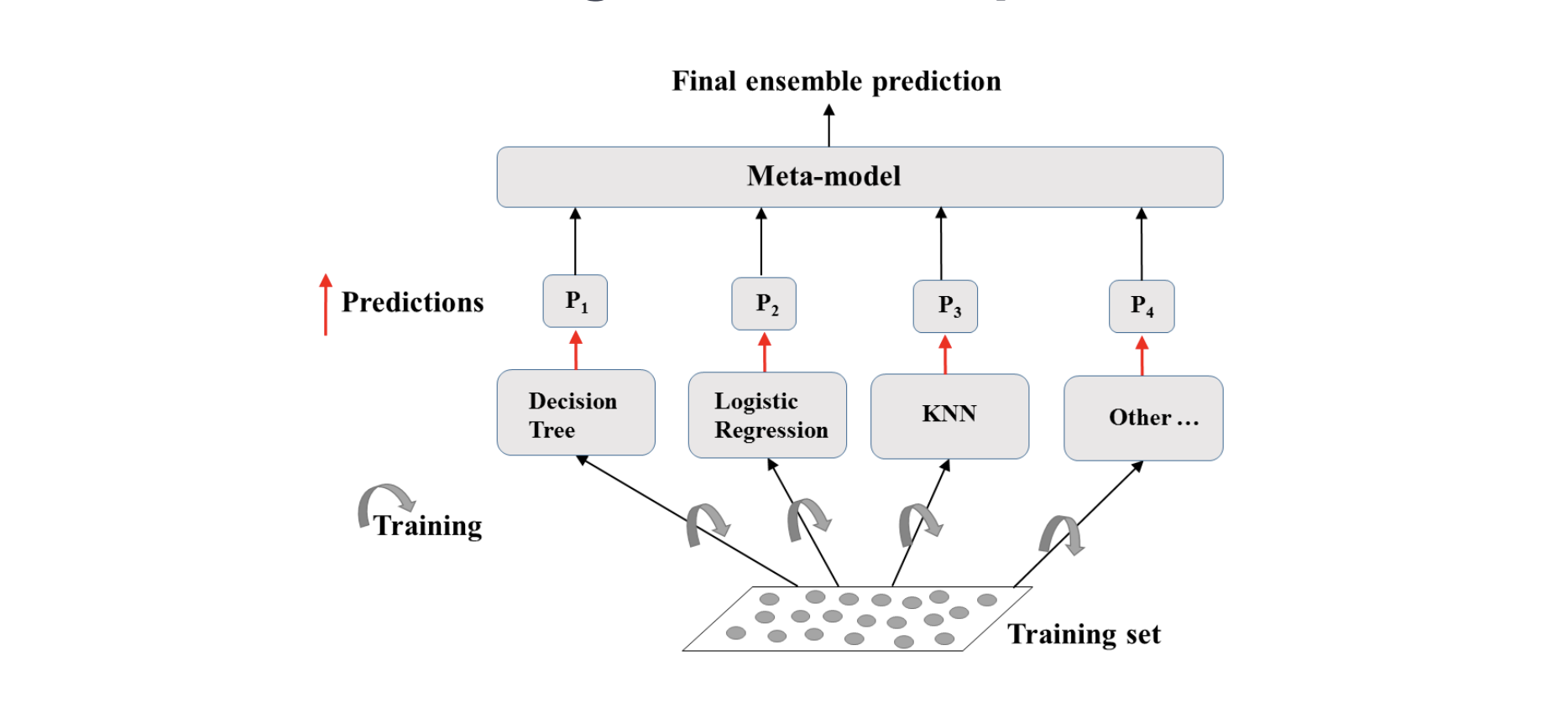
我们考虑一个Ensemble prediction的例子，叫做voting classifier，假设我们有i个预测器对同一组数据进行预测，产生i个结果叫做p1,p2,pi，结果只有两种，0或者1，i个结果都预测出来之后，我用投票的方式来觉得使用哪个结果，比如下面的图中，有两个预测器的结果是1，那么我们的结果就是1.

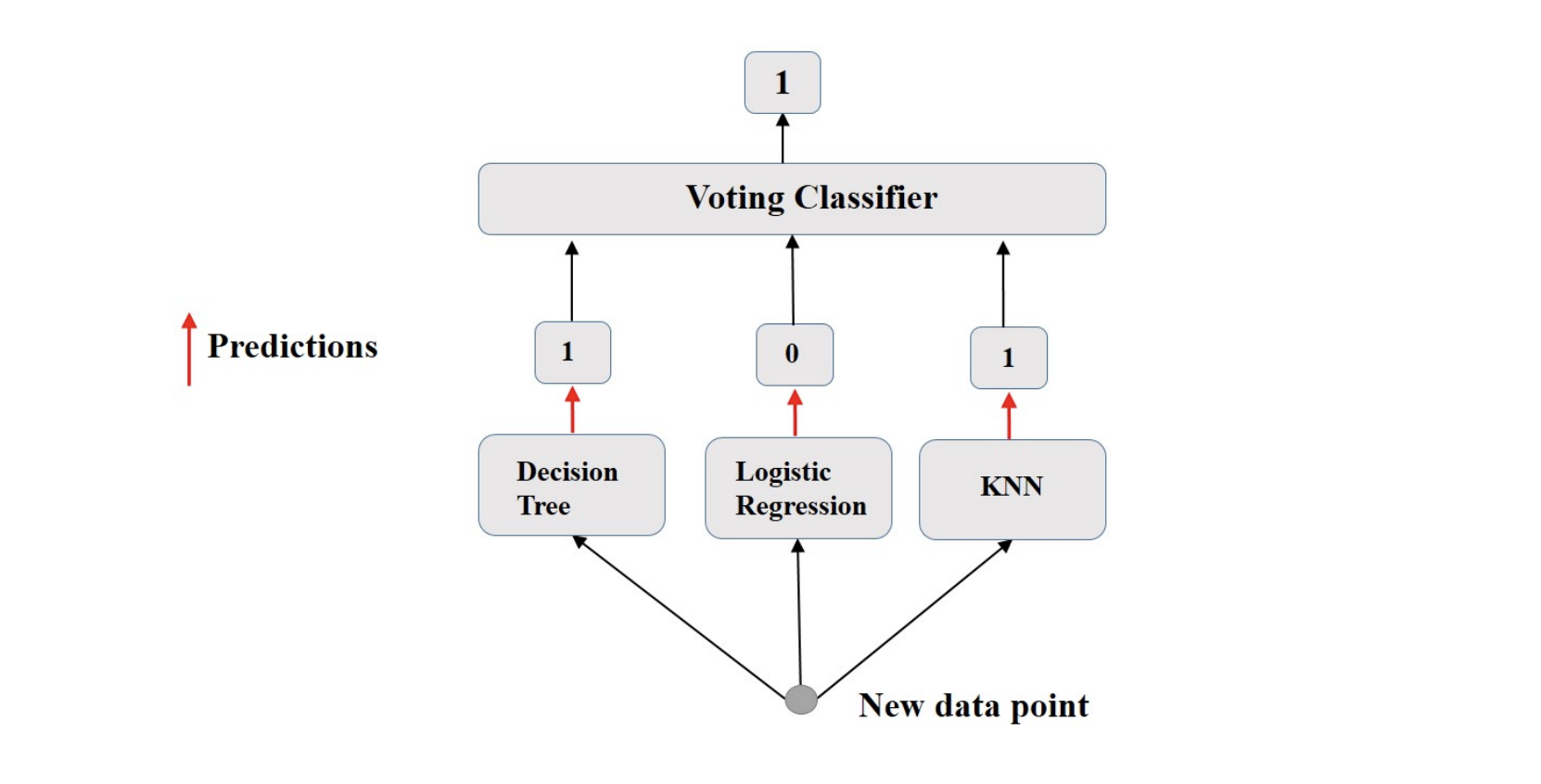
Ensemble Learning code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# Set seed for reproducibility
SEED=1

# Instantiate lr
lr = LogisticRegression(random_state=SEED)

# Instantiate knn
knn = KNN(n_neighbors=27)

# Instantiate dt
dt = DecisionTreeClassifier(min_samples_leaf=0.13, random_state=SEED)

# Define the list classifiers
classifiers = [('Logistic Regression', lr), ('K Nearest Neighbours', knn), ('Classification Tree', dt)]

# Iterate over the pre-defined list of classifiers
for clf_name, clf in classifiers:    
 
    # Fit clf to the training set
    clf.fit(X_train, y_train)    
   
    # Predict y_pred
    y_pred = clf.predict(X_test)
    
    # Calculate accuracy
    accuracy = accuracy_score(y_test,y_pred) 
   
    # Evaluate clf's accuracy on the test set
    print('{:s} : {:.3f}'.format(clf_name, accuracy))

Voting:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# Import VotingClassifier from sklearn.ensemble
from sklearn.ensemble import VotingClassifier

# Instantiate a VotingClassifier vc
vc = VotingClassifier(estimators=classifiers)     

# Fit vc to the training set
vc.fit(X_train, y_train)   

# Evaluate the test set predictions
y_pred = vc.predict(X_test)

# Calculate accuracy score
accuracy = accuracy_score(y_test, y_pred)
print('Voting Classifier: {:.3f}'.format(accuracy))

Bagging

‌Ensemble Learning 中，我们使用不同的算法对同一组数据进行处理再投票出结果，而 Bagging 正好相反，它用同一个算法，选取数据集中的不同组数据，计算结果，Bagging可以减少Variance。它和我们之前提及的 Bootstrap 方法类似。

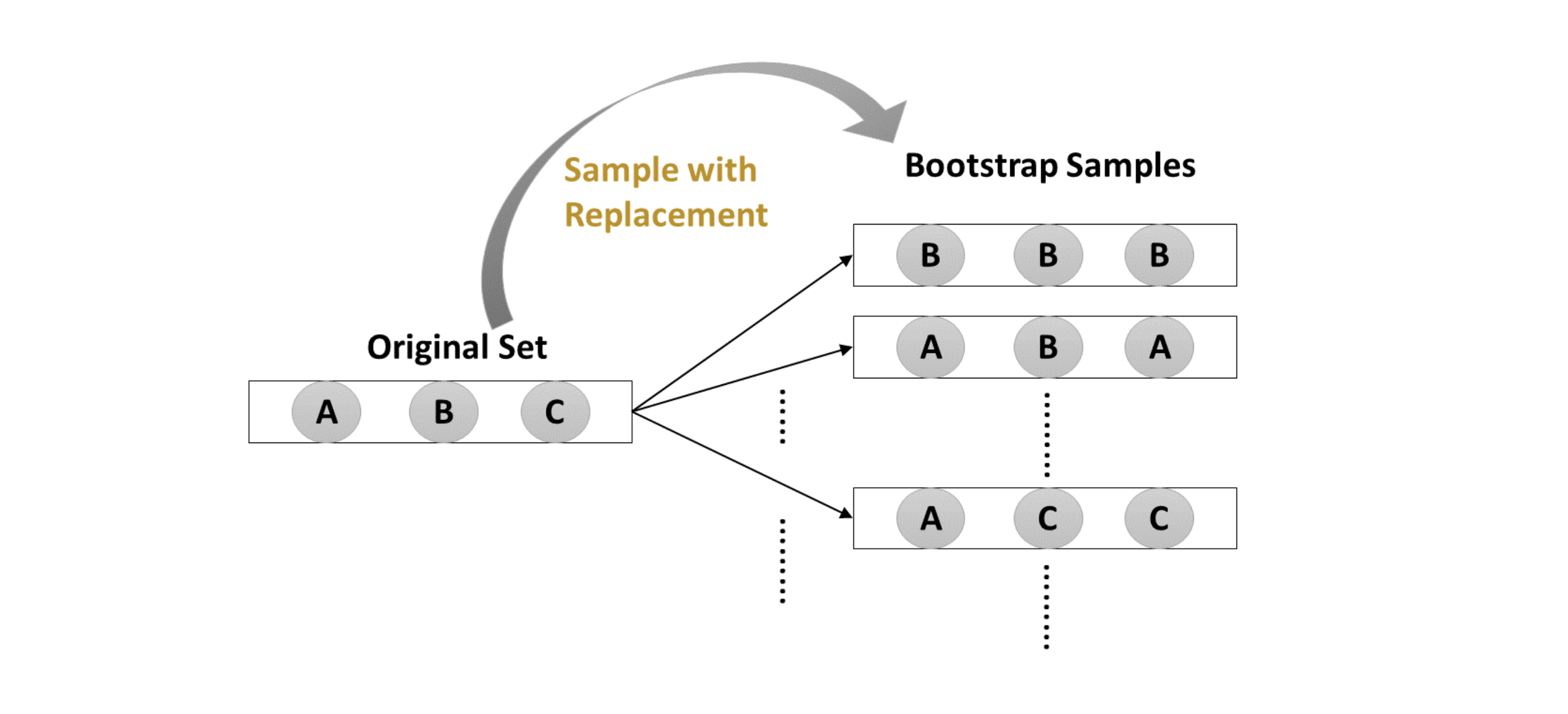
Bootstrap

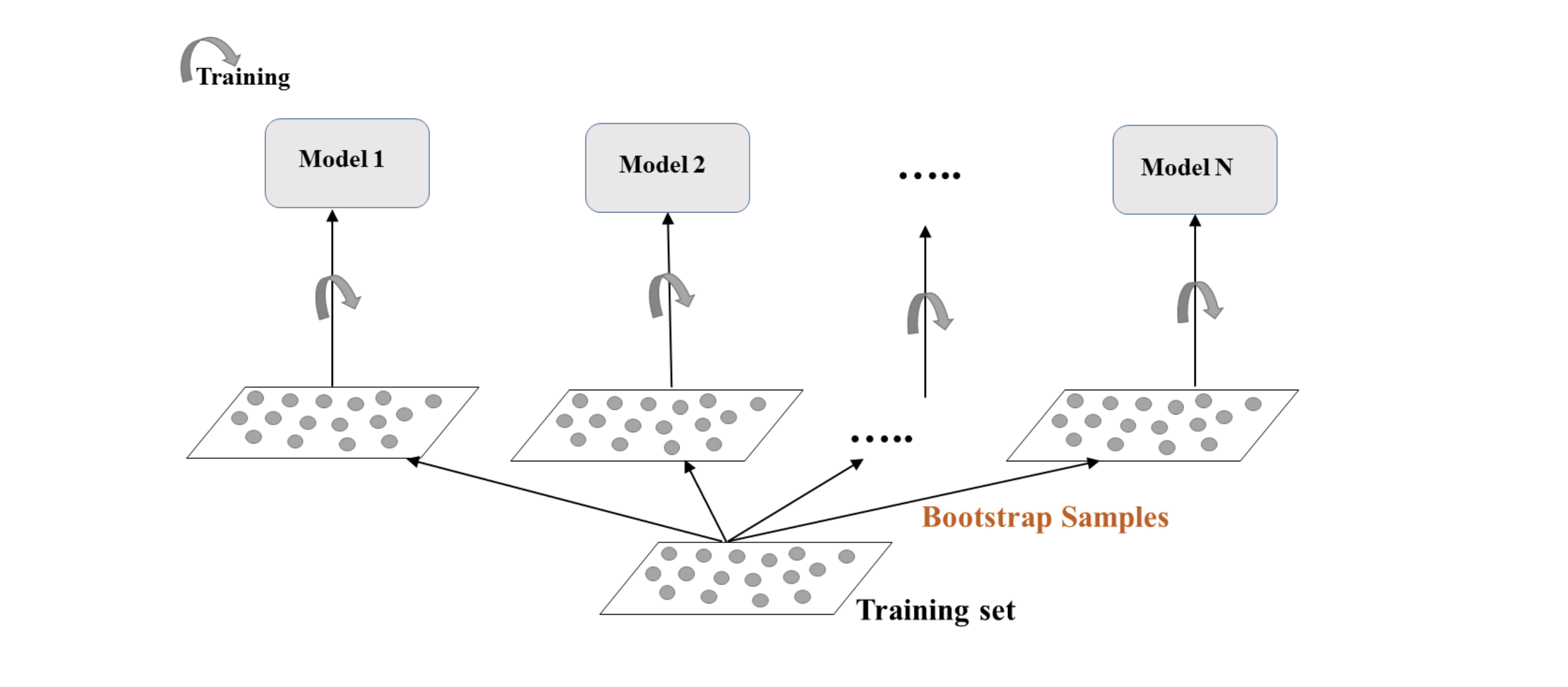
bagging不同model的结果，也是通过voting的出来的：

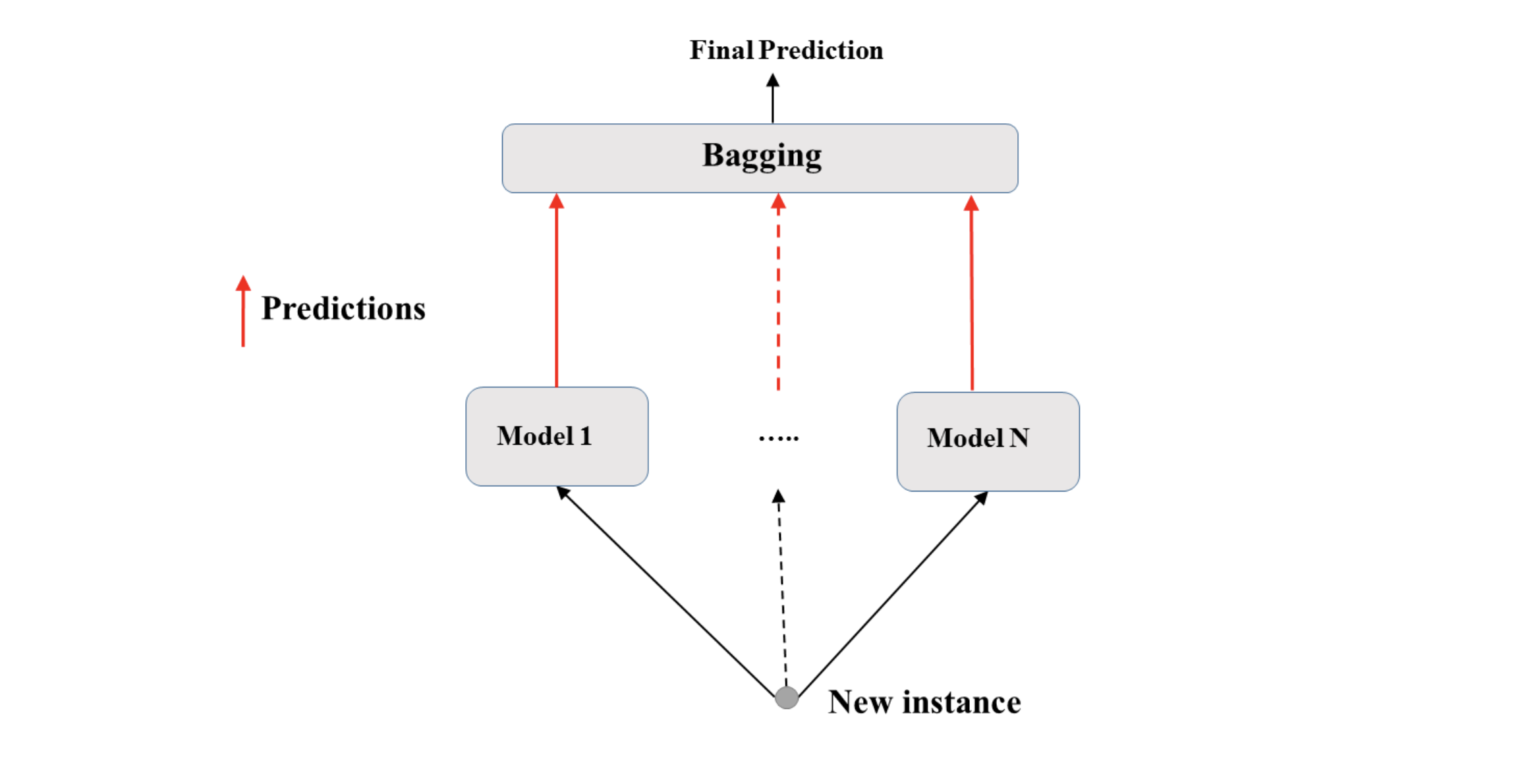
对于分类问题，结果通过major voting 获得，对于regression问题，结果通过平均结果获得。

Bagging python code:

1
2
3
4
5
6
7
8
9
10
11
# Import DecisionTreeClassifier
from sklearn.tree import DecisionTreeClassifier

# Import BaggingClassifier
from sklearn.ensemble import BaggingClassifier

# Instantiate dt
dt = DecisionTreeClassifier(random_state=1)

# Instantiate bc
bc = BaggingClassifier(base_estimator=dt, n_estimators=50,random_state=1)

Bagging performance:

1
2
3
4
5
6
7
8
9
# Fit bc to the training set
bc.fit(X_train, y_train)

# Predict test set labels
y_pred = bc.predict(X_test)

# Evaluate acc_test
acc_test = accuracy_score(y_test,y_pred)
print('Test set accuracy of bc: {:.2f}'.format(acc_test))

在 bagging 中，那些我们分割出来的test数据没有参与模型训练，这些模型没有见过的数据叫做 out of bag(OOB)，我们可以在每一次模型sample数据的时候，将这些数据分割为train和test数据组，如下图所示：

随机森林

随机森林也是一种基于决策树的算法，假设我们有一组心脏病数据，根据它来创建随机森林。

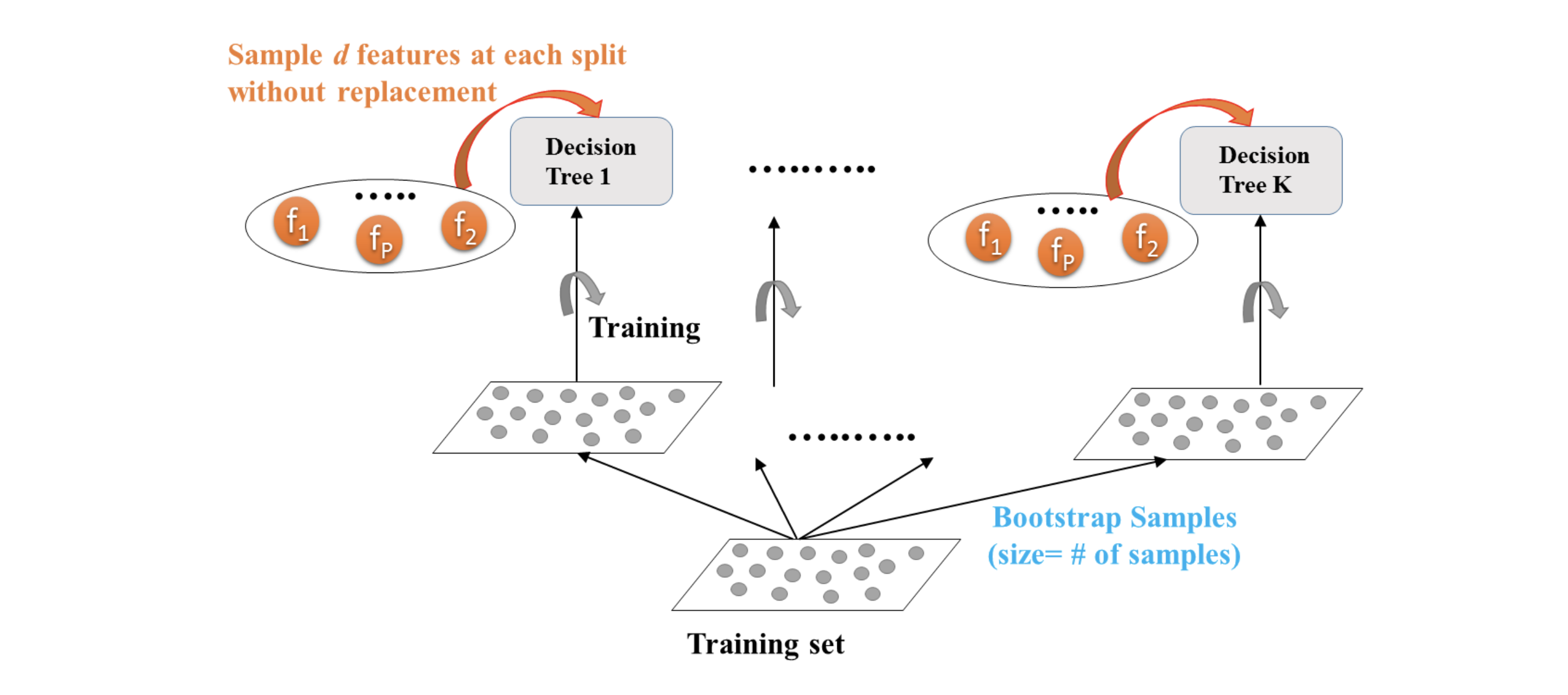
首先我们根据原始数据创建bootstrap dataset,即随机的（可重复）从原数据选择：

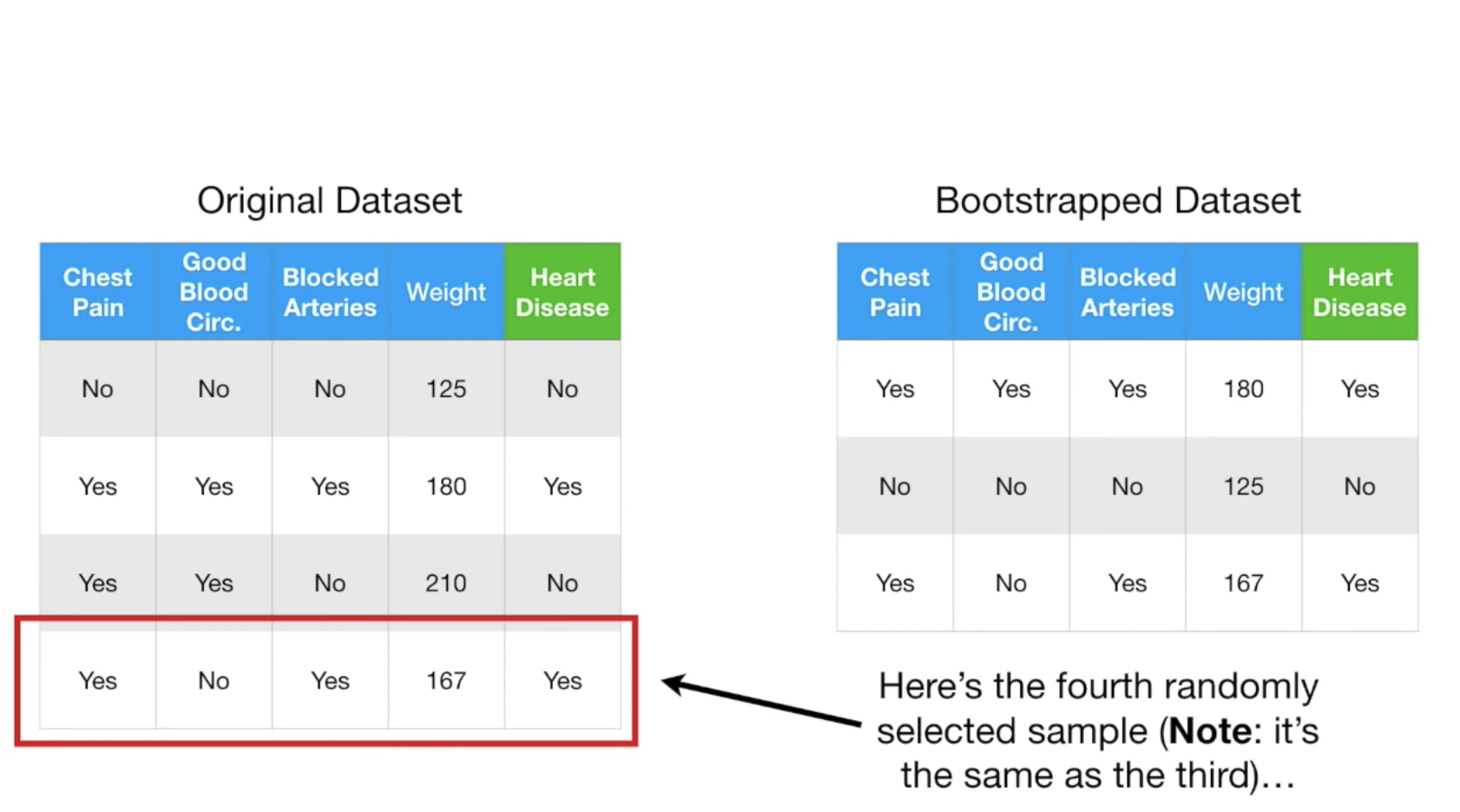
拿到随机创建的数据之后，我们随机的选择n个（这里暂时定为2个）feature，建立决策树，如何确定第一个树呢？可以根据gini算法，这里我们假设Good Blood最适合作为root节点，第一个树确定以后，我们可以再从剩下的树中随机的选择两棵树作为其他节点，示例图如下：

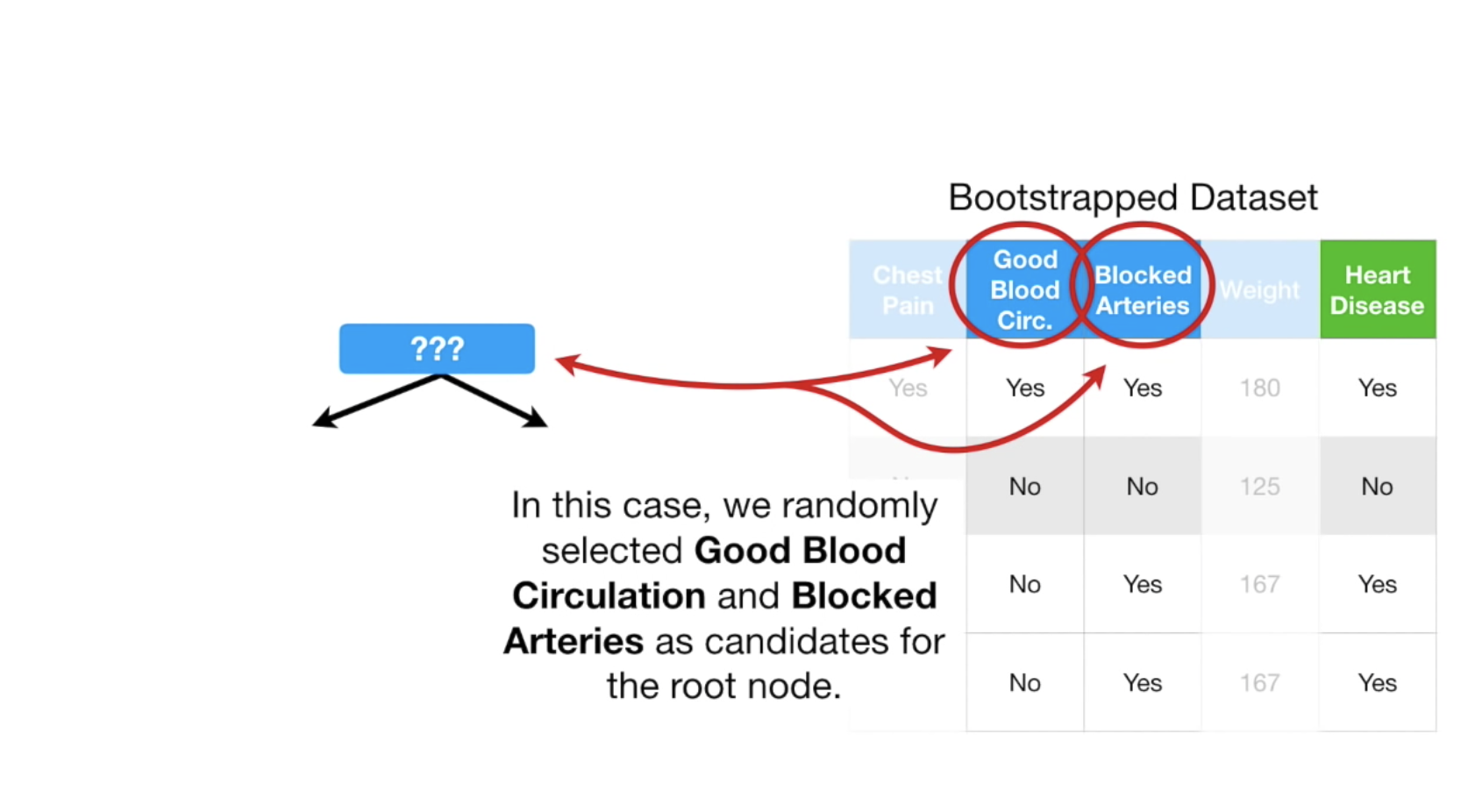
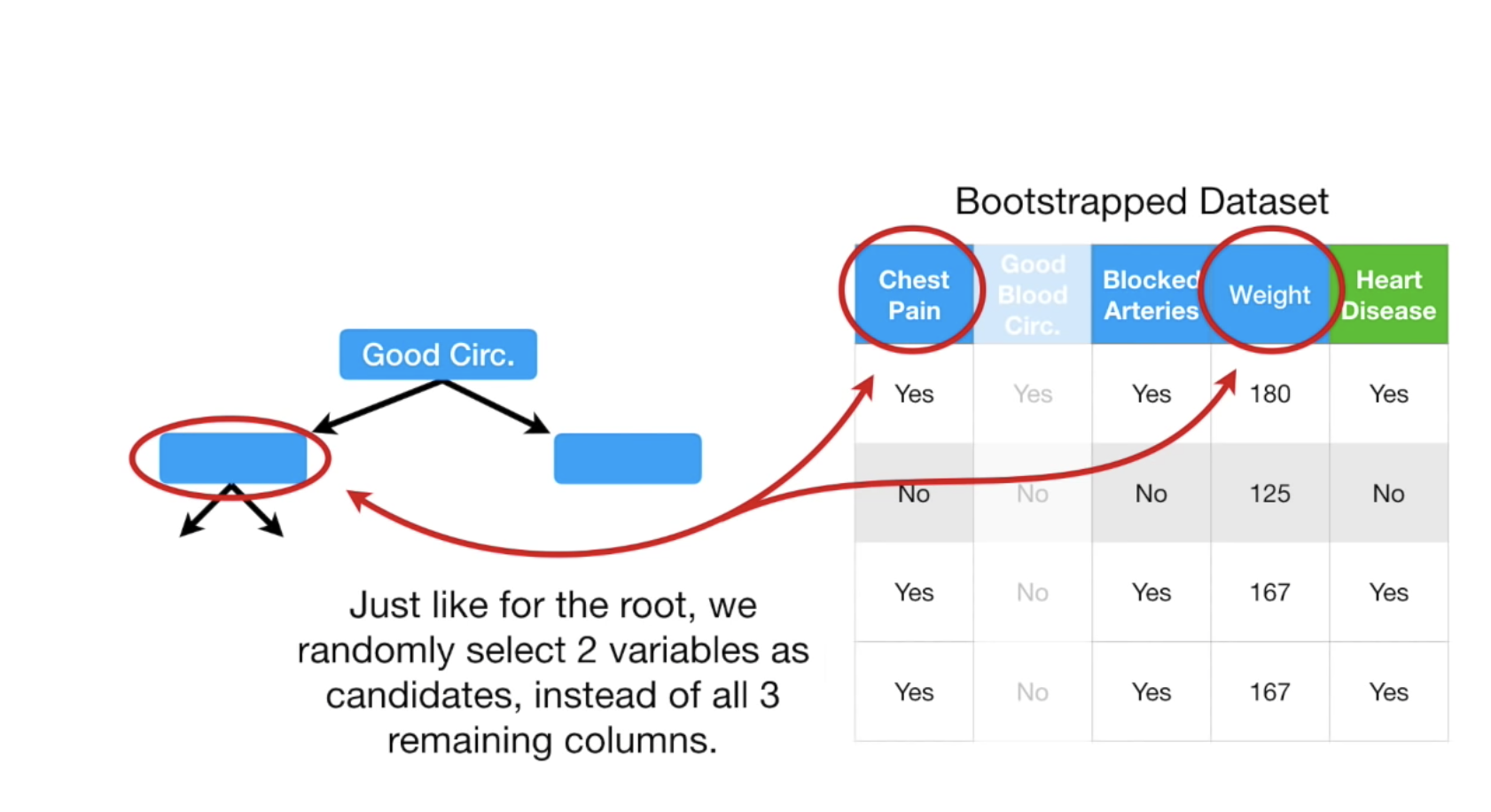
从剩下的树中选的时候，我们需要根据feature来选，根据哪些features来选， 以及多少features，都是需要提前定好的，在这里我们定为2。在sklearn中，是features的平方根，即如果我们有100个features，则每次用10个。

于是我们得到了一颗树，现在重复上述步骤，创建bootstrap数据，再建立树，这样我们可以重复很多次，于是随机森林就建立起来了。

随机森林建立好后，就可以开始预测，对于分类问题，我们使用投票机制决定输出，对于regresion问题，我们还是一样采用平均值。

随机森林python code：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# Import RandomForestRegressor
from sklearn.ensemble import RandomForestRegressor

# Instantiate rf
rf = RandomForestRegressor(n_estimators=25,
            random_state=2)
            
# Fit rf to the training set    
rf.fit(X_train, y_train) 

# Import mean_squared_error as MSE
from sklearn.metrics import mean_squared_error as MSE

# Predict the test set labels
y_pred = rf.predict(X_test)

# Evaluate the test set RMSE
rmse_test = MSE(y_test, y_pred)**(1/2)

# Print rmse_test
print('Test set RMSE of rf: {:.2f}'.format(rmse_test))

查看feature权重：

1
2
3
4
5
6
7
8
9
10
11
# Create a pd.Series of features importances
importances = pd.Series(data=rf.feature_importances_,
                        index= X_train.columns)

# Sort importances
importances_sorted = importances.sort_values()

# Draw a horizontal barplot of importances_sorted
importances_sorted.plot(kind='barh', color='lightgreen')
plt.title('Features Importances')
plt.show()