Scott's Blog

学则不固, 知则不惑

0%

机器学习：Classification and Regression Trees

发表于 更新于 分类于 阅读次数： Valine：

机器学习决策树的第一部分，分类与回归树（CART）的原理（多图)。

介绍

为什么使用决策树呢，主要有两个原因，一是决策树通常模仿人类的思维，因此它很容易理解数据并做出一些很好的解释。二是决策树可以让你看到数据的逻辑。

我们看一个金融机构决定是否投资一家公司决策树：

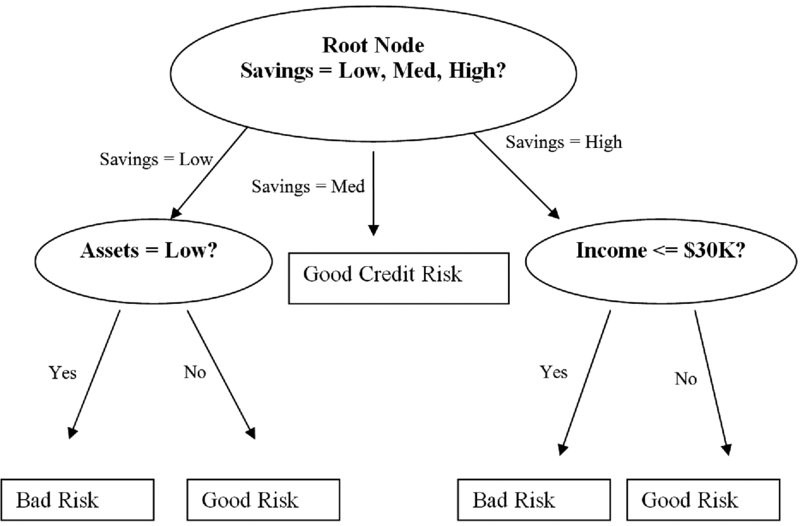
从决策树的组成来看，它是由一系列节点（nodes）的继承关系组成的，节点可以看作是对问题做出回答，也可以是问题的答案。这些问题有些依据数据的分类，如你是否吸烟，有的是数据本身你一天吸几根，（数值型），决策树中主要有三类节点：

  1. Root, root节点没有父节点，有两个子节点
  2. Internal root, 一个父节点，两个子节点
  3. Leaf, 一个父节点，没有子节点

每一个internal root代表一个“test” on an attribute，即在这个节点根据这个属性做出的判断，每一个分支则代表了判断的输出，每一个leaf代表了一个class label，即最后的决定。

下面是一些决策树中的常见名词：

  1. Root Node: It represents entire population or sample and this further gets divided into two or more homogeneous sets.
  2. Splitting: It is a process of dividing a node into two or more sub-nodes.
  3. Decision Node: When a sub-node splits into further sub-nodes, then it is called decision node.
  4. Leaf/ Terminal Node: Nodes do not split is called Leaf or Terminal node.
  5. Pruning: When we remove sub-nodes of a decision node, this process is called pruning. You can say opposite process of splitting.
  6. Branch / Sub-Tree: A sub section of entire tree is called branch or sub-tree.
  7. Parent and Child Node: A node, which is divided into sub-nodes is called parent node of sub-nodes whereas sub-nodes are the child of parent node.

决策树如何学习

要建立决策树，就得对数据进行分类，第一个节点即根节点的分类范围是最大的，它把所有的问题分成两类。

如何找到这个分类呢？这取决于那些最能对数据集进行分类的属性，怎么确定哪些分类最能对数据进行分类呢？

看下面一个心脏病的例子，我们把每一个分类的都单独拿出来，计算分别统计它相对结果的预测量，如下图：

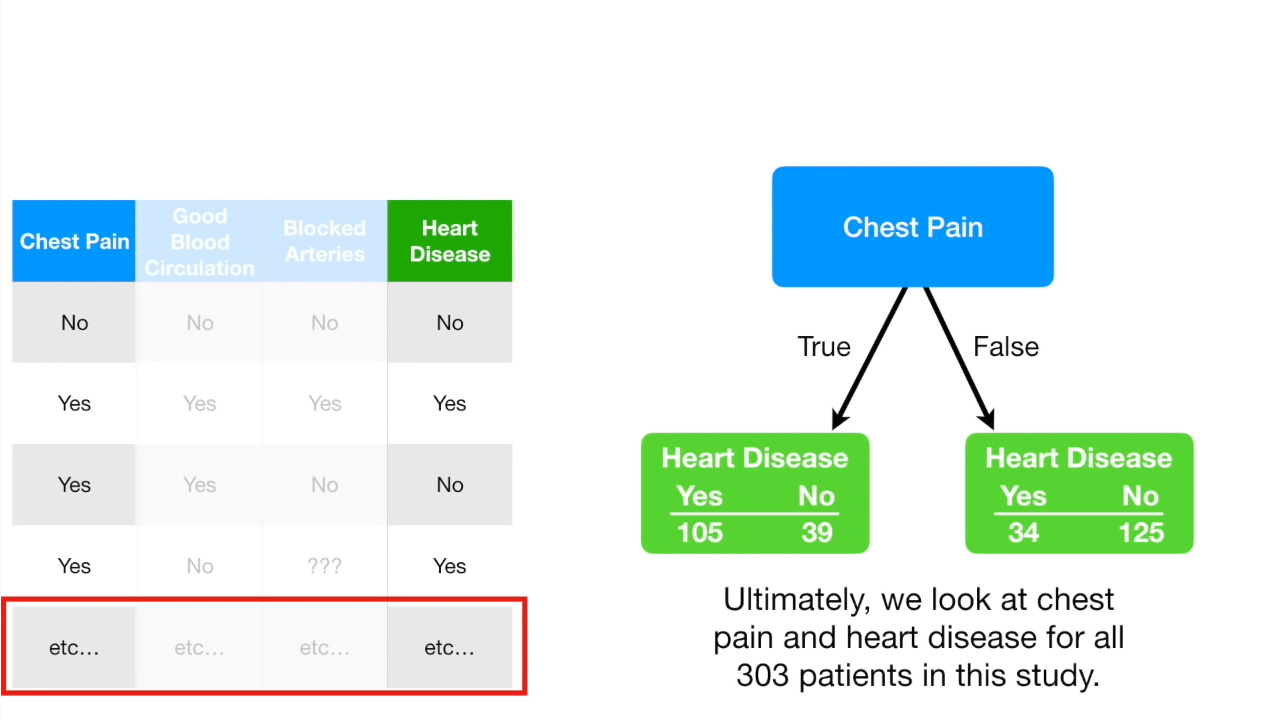
有没有心脏病是我们的leaf，也就是结果输出，而胸痛是feature。我们统计胸痛的值与现有的心脏病的值的对应关系，如果胸痛，是否是心脏病？如果胸不痛，是否是心脏病？这样我们就得到四列数据，结束对胸痛这个feature的统计后，继续对Good Blood进行同样的操作。

可以看到这个结果中，不管是胸痛，还是血液情况，都没办法在yes与no后就准确预测心脏病，所以上面的这些数据都是impurity的，那我们如何衡量这种impurity的程度呢？

有很多衡量 impurity 的方法，其中一种叫做Gini, 下面是Gini的计算方式：

同样的方法计算右边的节点:

但是左右两边的患者数量是不一样的，一个是144,一个是159:

我们需要对左右节点都平均一下再相加：

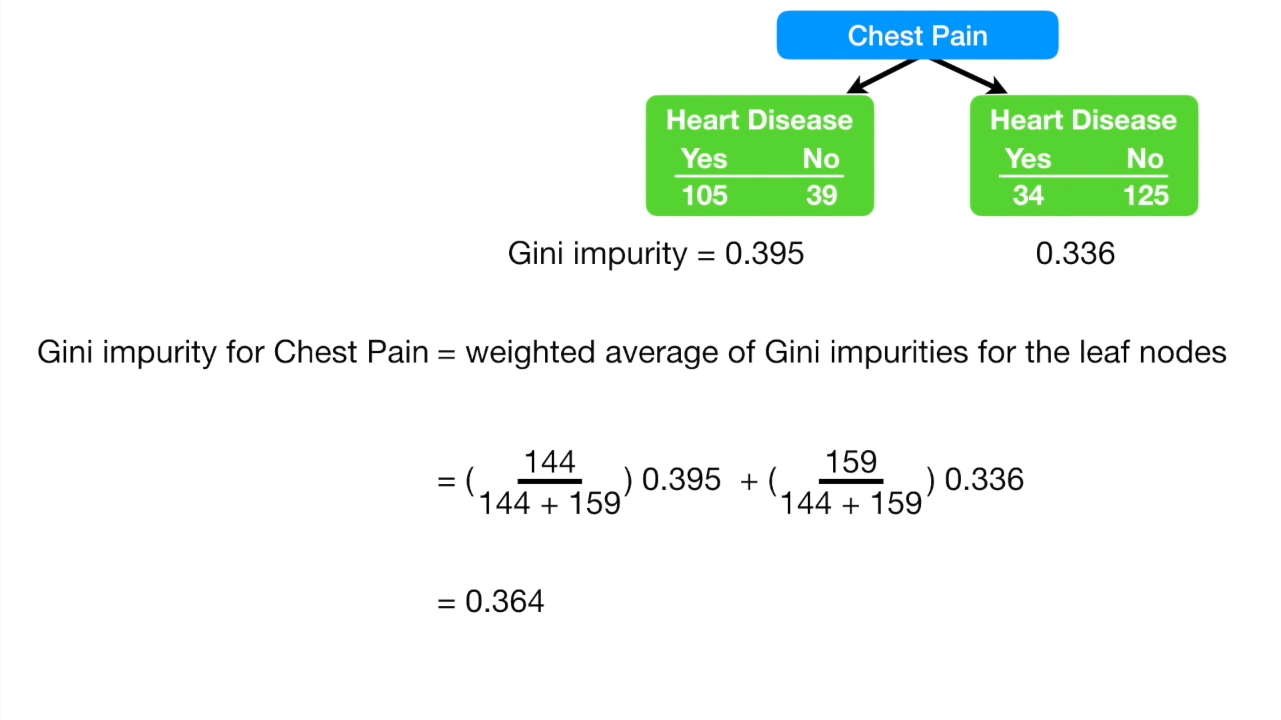
再把所有的feature都算一遍，

我们选择gini数最低的那个一，作为root node

root node确定了之后，我们还需要确定后续的节点使用哪个feature，这个步骤和前面确定root node是一样的：

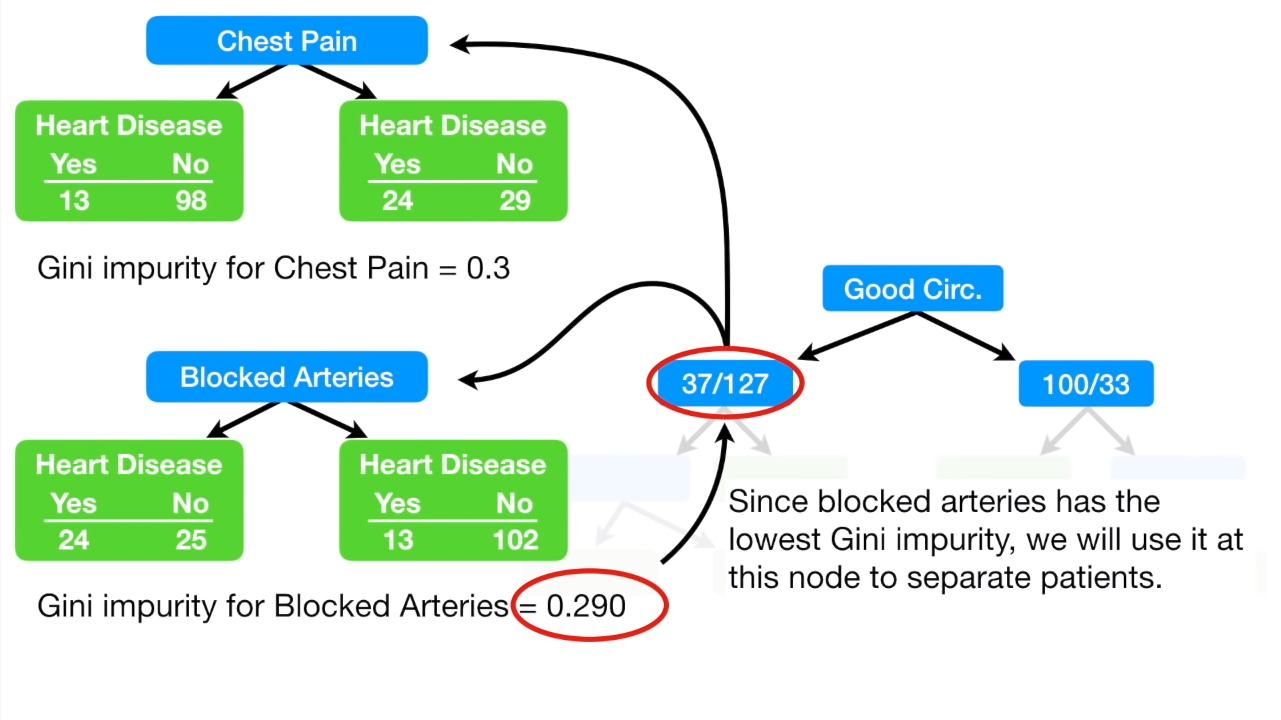
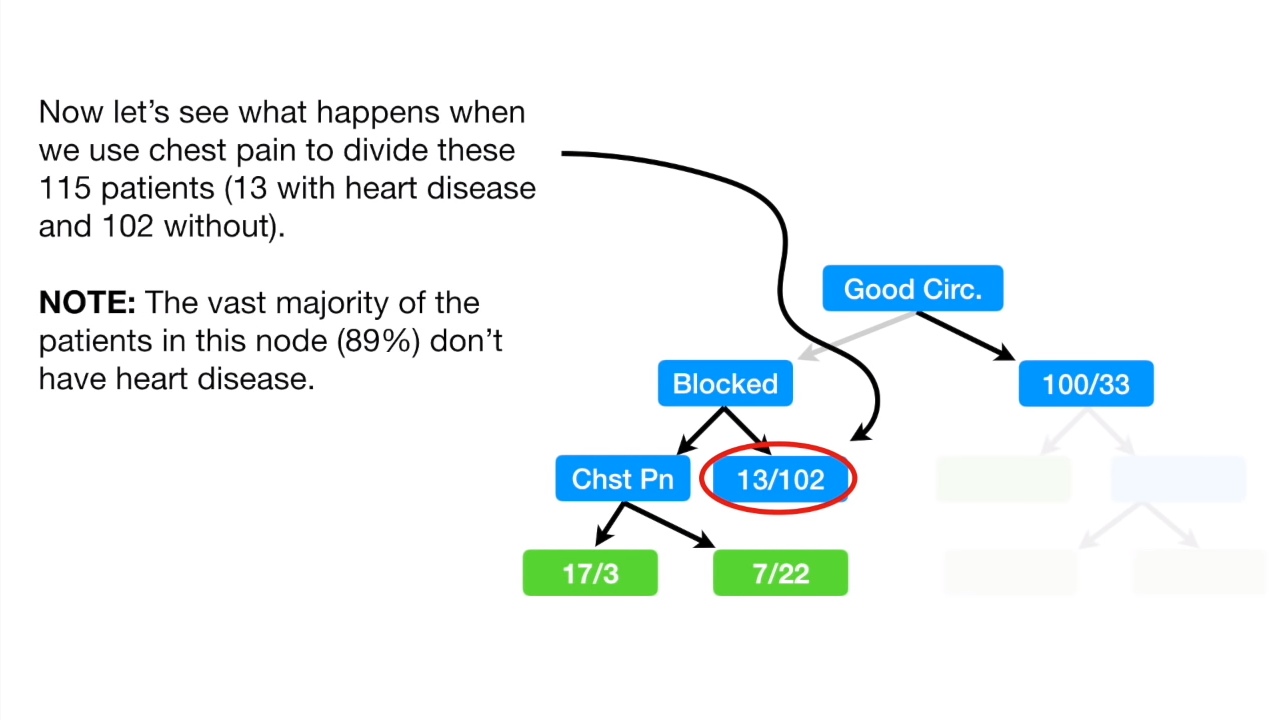
进一步往下面确定子节点的时候，我们发现，在动脉阻塞(blocked)的两个子节点下， 没有发生动脉阻塞这个节点中，只有13个患有心脏病，也就是说89%的患者都没有心脏病！

我们来算一下这个节点的gini值与进一步按照胸痛往下面细分后的gini值：

可以看到按照胸痛细分后的gini值为0.29，而不细分的值则为0.2，所以对于这个节点来说，就没有必要再往下面细分节点了，所以我们就不处理 13/102 这个节点了，它也就成了我们说的 leaf 节点。

将剩下的部分以及右边的子节点补上，我们的决策树就建好了:

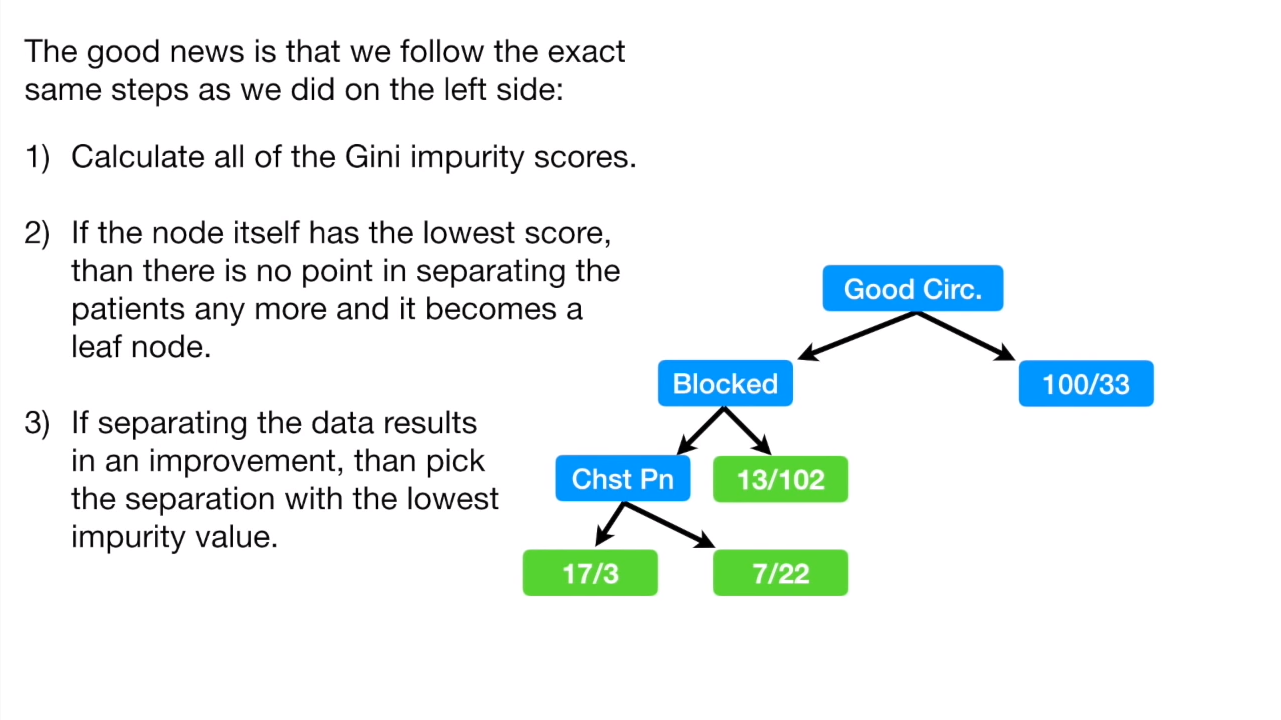
不过还有一个问题，我们前面都是基于yes or no的问题，那如果遇到数值型的数据怎么办？

首先，我们将数值数据从小到大排列：

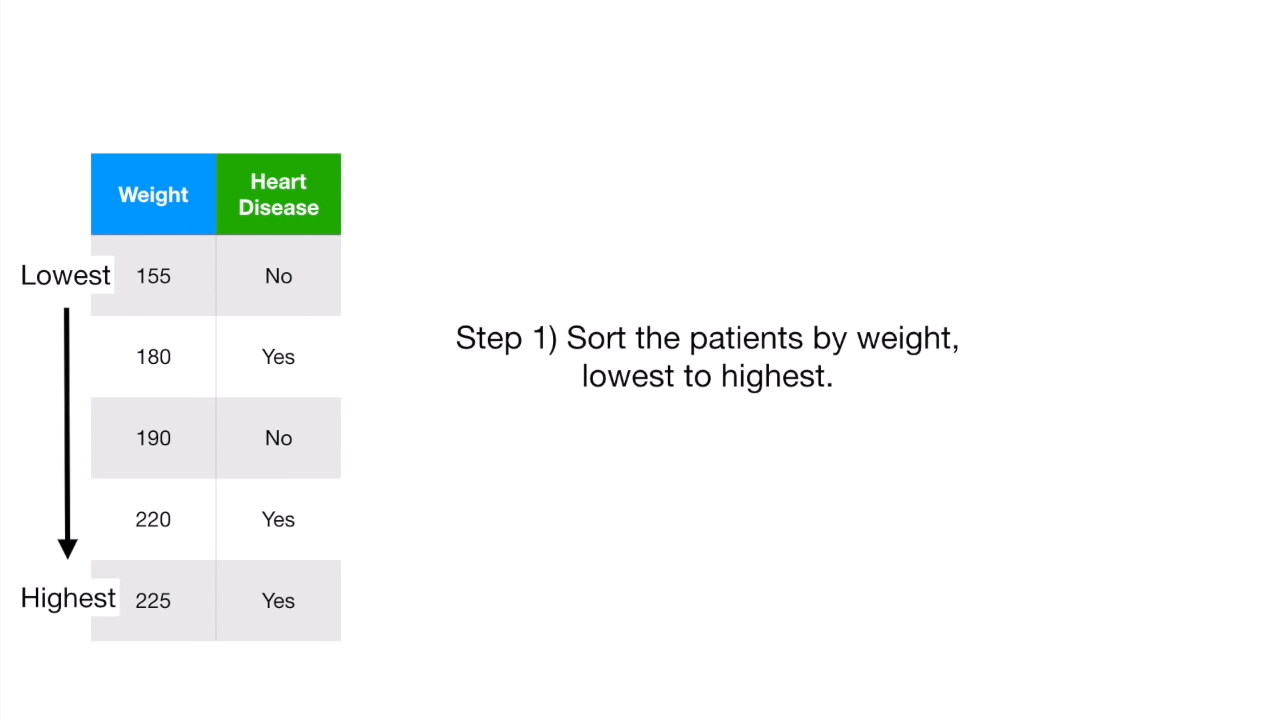
两两取数值中间的平均值，计算gini值：

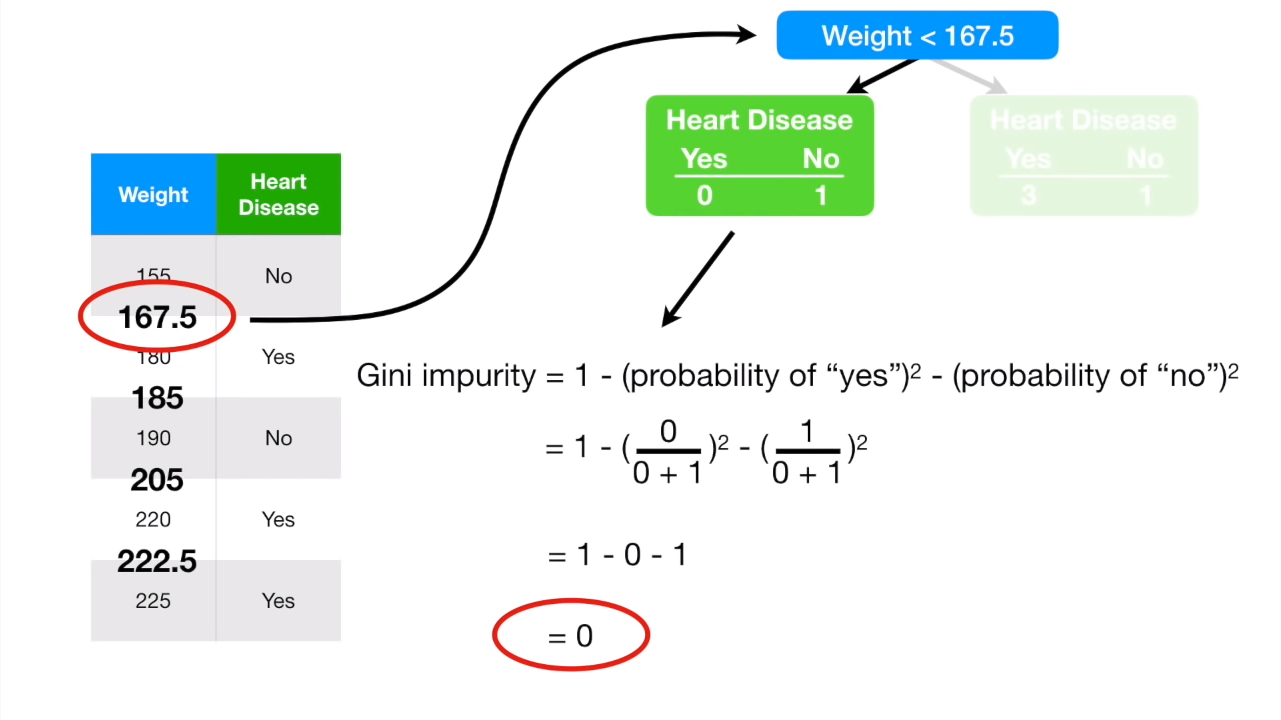
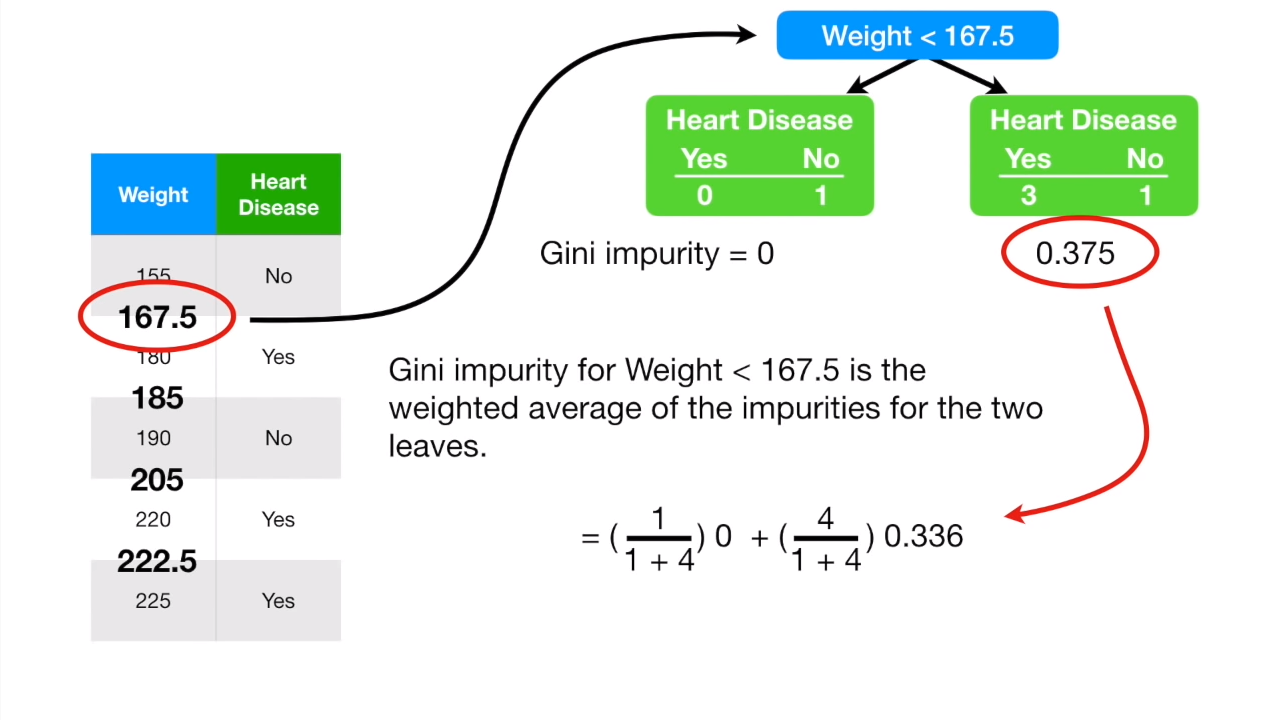
重复计算所有其他的gini值，最后选出最小的那个。

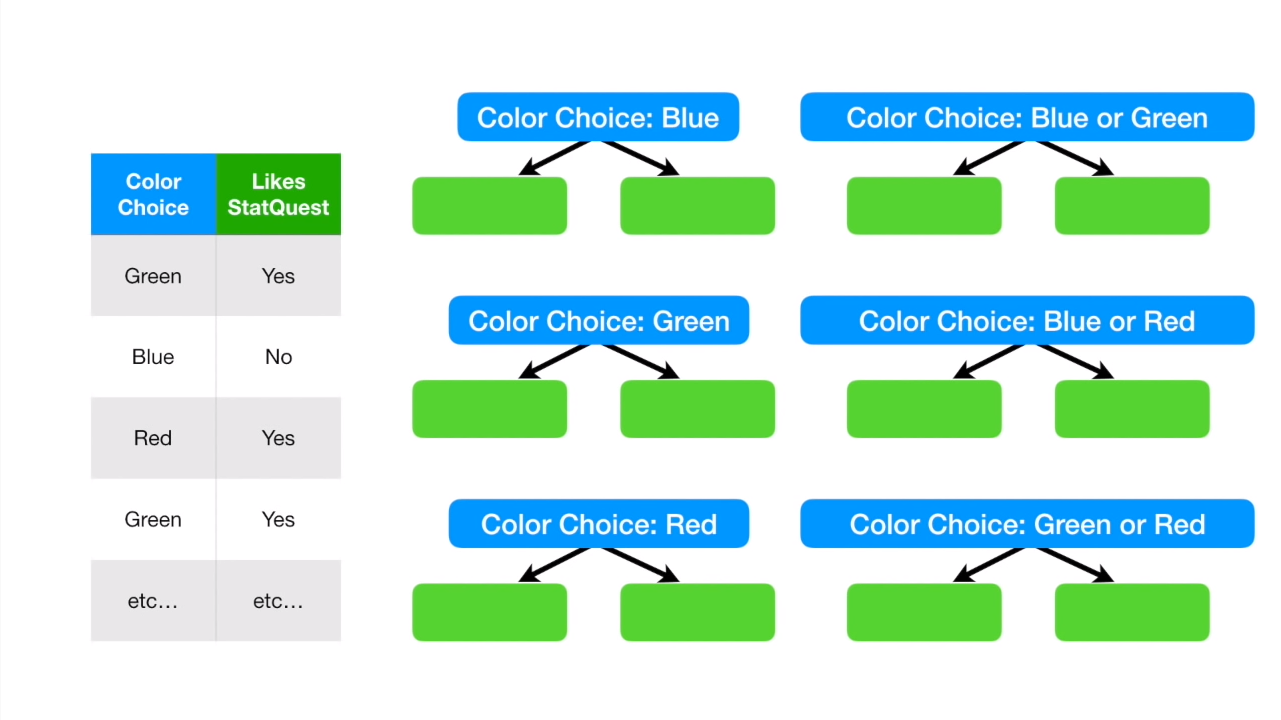
这就是数值型数据的计算了。不过还有一些数据它是选择型的，如颜色的选择，对于颜色的选择，我们可以把选择分开来计算，如下图：

关于决策数的视频

上面的这个gini值，我们又叫做IG(Information Gain)值，我们知道，如果IG值为0，或者我们发现该node分割后gini值更高，我们就不继续分割，该node就叫做leaf。如果我们固定了一颗数的深度，那么当分割node的时候，超过了规定的深度，我们也会停止分割子节点。

另外，拆分内部节点总是涉及最大化信息增益！

使用决策树

决策树可以解决classfication问题，也可以解决regression问题，我们先讨论分类树。

训练决策树：

1
2
3
4
5
6
7
8
9
10
11
12
# Import DecisionTreeClassifier from sklearn.tree
from sklearn.tree import DecisionTreeClassifier

# Instantiate a DecisionTreeClassifier 'dt' with a maximum depth of 6
dt = DecisionTreeClassifier(max_depth=6,random_state=SEED)

# Fit dt to the training set
dt.fit(X_train, y_train)

# Predict test set labels
y_pred = dt.predict(X_test)
print(y_pred[0:5])

决策树评分：

1
2
3
4
5
6
7
8
9
# Import accuracy_score
from sklearn.metrics import accuracy_score

# Predict test set labels
y_pred = dt.predict(X_test)

# Compute test set accuracy  
acc = accuracy_score(y_pred, y_test)
print("Test set accuracy: {:.2f}".format(acc))

逻辑回归与分类树:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# Import LogisticRegression from sklearn.linear_model
from sklearn.linear_model import  LogisticRegression

# Instatiate logreg
logreg = LogisticRegression(random_state=1)

# Fit logreg to the training set
logreg.fit(X_train, y_train)

# Define a list called clfs containing the two classifiers logreg and dt
clfs = [logreg, dt]

# Review the decision regions of the two classifiers
plot_labeled_decision_regions(X_test, y_test, clfs)

分类树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# Import DecisionTreeClassifier from sklearn.tree
from sklearn.tree import DecisionTreeClassifier

# Instantiate dt_entropy, set 'entropy' as the information criterion
dt_entropy = DecisionTreeClassifier(max_depth=8, criterion='entropy', random_state=1)

# Fit dt_entropy to the training set
dt_entropy.fit(X_train, y_train)

# Import accuracy_score from sklearn.metrics
from sklearn.metrics import accuracy_score

# Use dt_entropy to predict test set labels
y_pred = dt_entropy.predict(X_test)

# Evaluate accuracy_entropy
accuracy_entropy = accuracy_score(y_test, y_pred)

# Print accuracy_entropy
print('Accuracy achieved by using entropy: ', accuracy_entropy)

# Print accuracy_gini
print('Accuracy achieved by using the gini index: ', accuracy_gini)

回归树

1
2
3
4
5
6
7
8
9
10
# Import DecisionTreeRegressor from sklearn.tree
from sklearn.tree import DecisionTreeRegressor

# Instantiate dt
dt = DecisionTreeRegressor(max_depth=8,
             min_samples_leaf=0.13,
            random_state=3)

# Fit dt to the training set
dt.fit(X_train, y_train)

衡量回归树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# Import mean_squared_error from sklearn.metrics as MSE
from sklearn.metrics import mean_squared_error as MSE

# Compute y_pred
y_pred = dt.predict(X_test)

# Compute mse_dt
mse_dt = MSE(y_test, y_pred)

# Compute rmse_dt
rmse_dt = mse_dt**(1/2)

# Print rmse_dt
print("Test set RMSE of dt: {:.2f}".format(rmse_dt))

Linear regression vs regression tree

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# Predict test set labels 
y_pred_lr = lr.predict(X_test)

# Compute mse_lr
mse_lr = MSE(y_test, y_pred_lr)

# Compute rmse_lr
rmse_lr = mse_lr**(1/2)

# Print rmse_lr
print('Linear Regression test set RMSE: {:.2f}'.format(rmse_lr))

# Print rmse_dt
print('Regression Tree test set RMSE: {:.2f}'.format(rmse_dt))