概率与统计的基础概念。

统计

数据类型：

离散类型，只能是某些既定的值
连续类型，可以是一个范围里任何的值

离散数据是数出来的，连续数据是测量出来的。对于离散概率分布，我们关心的是取得一个特定数值的概率。例如抛硬币正面向上的概率为:p(x=正面)=1/2

而对于连续概率分布来说，我们无法给出每一个数值的概率，因为我们不可能列举每一个精确数值。

1. Histograms（直方图）

定义：是一种对数据分布情况的图形表示，横轴是统计样本，纵轴是统计样本某个属性的度量。

我们测试人的身高，把这些数据放到数轴上，并分段，把数据这个段（bins）的数据从下往上堆，就得到了直方图。

有了这个图，我们就可以预测未来的到某个身高值的概率。

比如，你敢打赌下一个测量的人，有很大的几率处在直方图靠近中间的位置。

如果你想要用一个图，来近似表示你的数据，或未来预测的测量值，就可以使用直方图。

直方图中的bins的选择，很重要，太小或太大都不行，不要仅仅依靠程序的默认值。

2. Statistical distribution（概率分布）

现在你拿到了直方图，你的bins可能需要调整一下，你从1调整为0.5，这样让你的图像更直观，同时，也让你对数据的预测更准确。

你会发现，你的数据量越多，和你的bins越小，都可以提高你对数据预测的准确率。

你可以用一条曲线来表示分布，他比直方图更准确，因为直方图总会有在某个区间的值比较少或没有的情况，而曲线是连续的，且很方便计算。

另外，当你没有足够的资源和钱做足够的测试，你其实可以用既有的数据算出这跟我曲线。曲线图和分布图都是描述分布的一种方式。

3. Normal Distribution（正态分布）

我们看过身高的数据，会发现它是左右对称的，事实上人类身高是一种正态分布。

刚出生的小孩和成年人的分布不一样，成年人高矮的区间比较大，而刚出生的小孩身高区间都在一个比较小的范围。

这个分布的宽度（即身高的区间）由数据的标准差决定。

知道这个标准差很重要，如在小孩的分布中，图像标准差为0.6，成人的为4.

我们可以知道 95% 的数据会落在（平均值 +- 2* 标准差），自然界的很多事物都遵循正态分布，这是因为什么呢？这就是中心极限定理

4. Population Parameters（总体参数）

我们选择测量一些基因数据，得到了一个直方图，通过直方图计算概率。

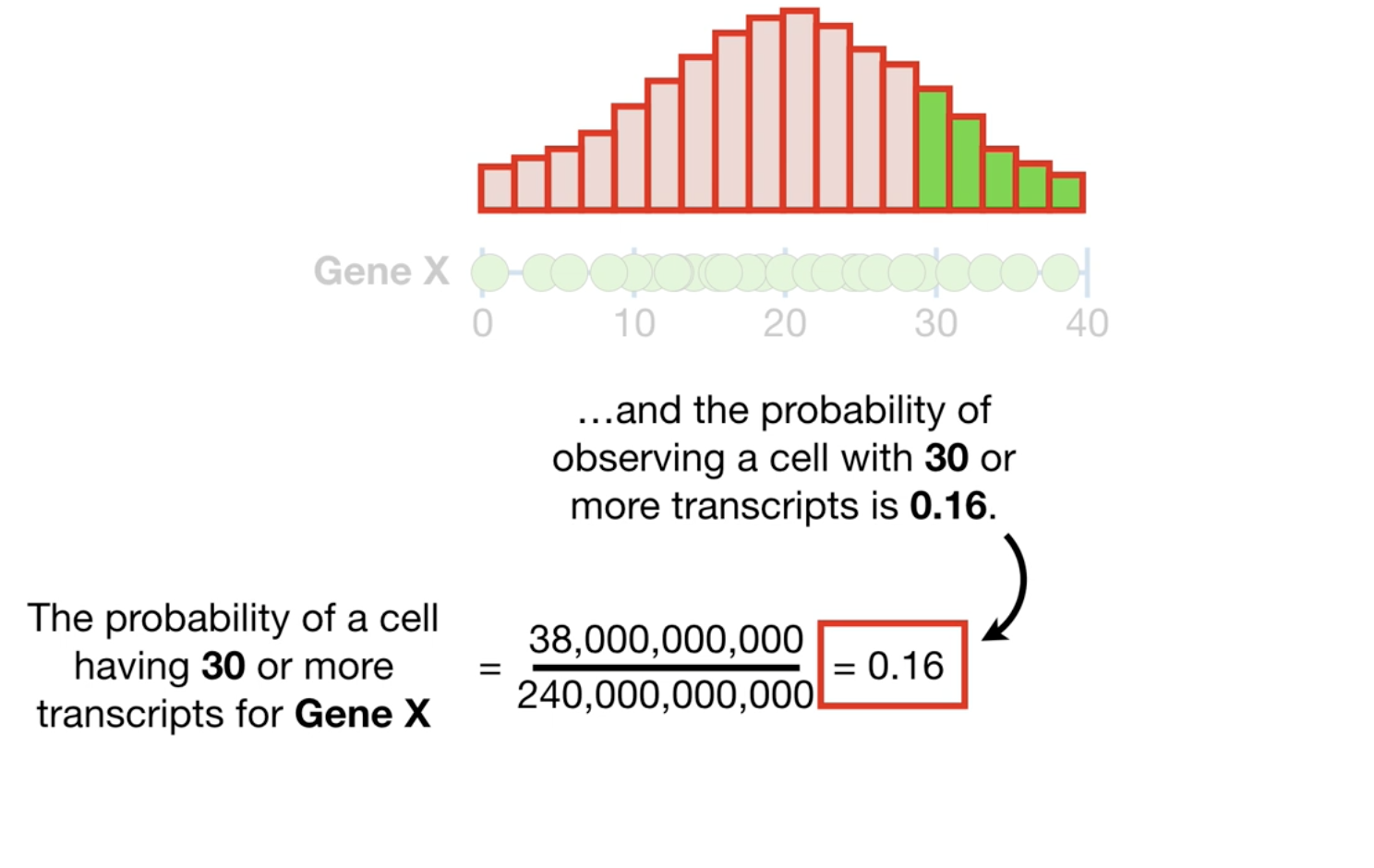
这个分布的 mean=20, std=10。

同样的，我们也可以根据曲线图来计算概率。

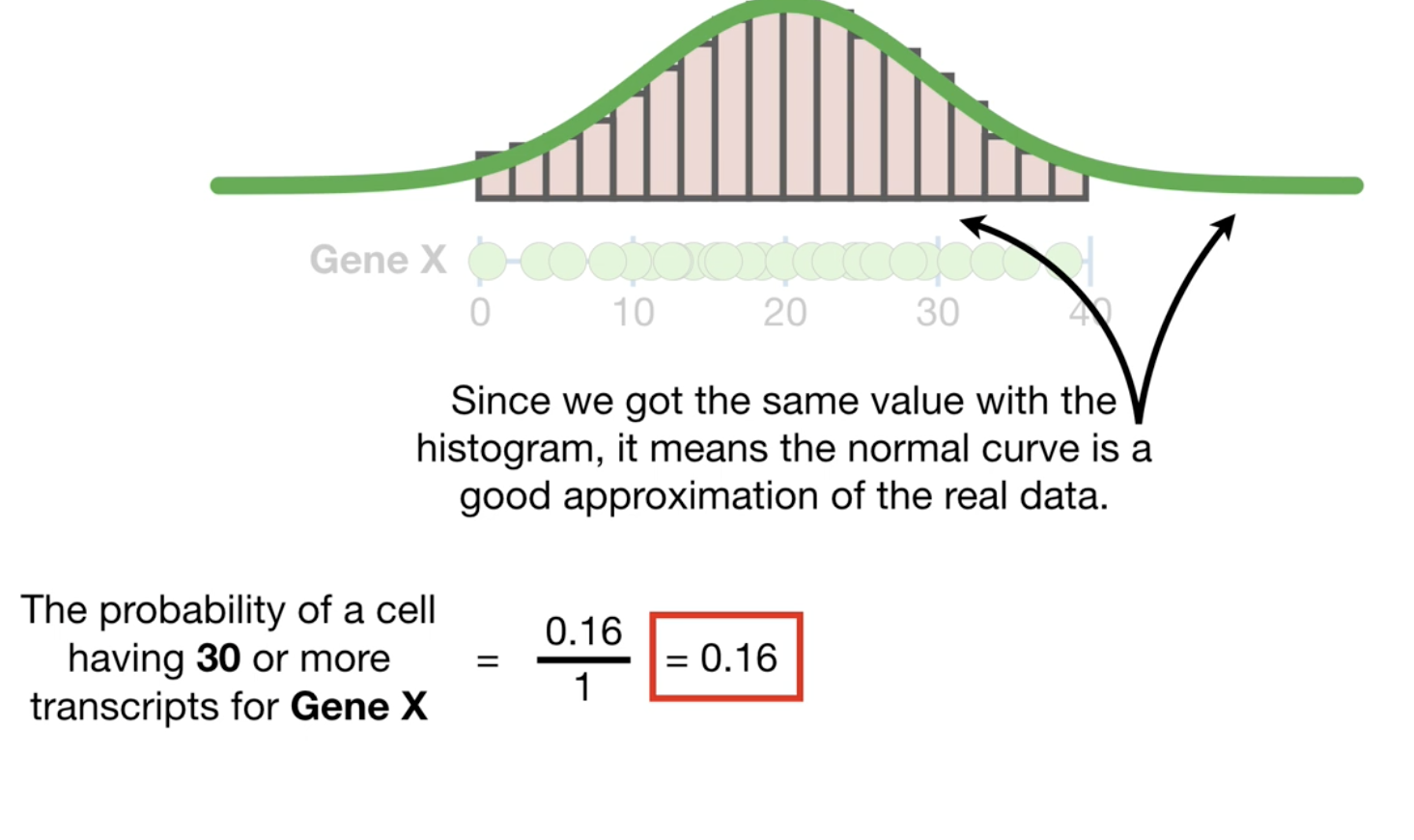
因为上述的直方图和曲线图，表示了所有的基因数据分布，在统计上会叫它为population，而mean和std，叫做 population mean 和 population std.

分布有很多种，有：

指数分布，指数分布的参数是rate,即population rate.
Gamma 分布, 参数是 shape 和 rate

知道 population 参数的原因是，你的分布可以重复计算. 如果你有机器学习基础，你可以把 population参数看作是 training dataset, 曲线则是我们想要根据我们的方法作出的预测。

事实上，你测量的数据得到的population参数，每次都是不一样的，那怎么估计真实的参数呢？事实上，当你做的测量越多，你得到的参数，就越接近真实的参数。

统计的一个目的就是，根据你现有测量的数据，你对这个真实的参数，有多大的信心估计正确了。

特别的，我们一般用 p-value 和置信区间来描述这种信心。

数据也多，你的信心就越大，

bootstrap refresher

我们测量12只母老鼠的体重，并计算这组老鼠体重的的平均值，这个平均值只是这12只老鼠的，而利用sample，我们可以利用手中已有的值，去估计所有老鼠体重的平均值。

怎么做的，用 sampling with replacement，即有放回的抽样，抽12次之后，计算平均值。

重复上面的步骤很多次，对这些平均值再取平均，即得到了你想要的值。

再来说置信区间，我们一般说95%的置信区间，意思就是，那个包含了上述95%的平均值的范围。

如果你拿母老鼠和公老鼠的数据对比，分别看他们95%的平均值的范围，如果彼此没有重合，那就可以说他们是不一样的，两组值的mean是统计显著的，而如果有重合的部分，就需要做t-test了。

5. Mean，Variance，STD

我们以上面的基因例子为例，对240万个基因值计算平均值，即得到了平均值，注意，这是对所有的值计算平均值，所以不是population mean，而是真正的mean。

注意区分：

sample mean，estimated mean（x-bar）
population mean（mu）

总结：

如果你有所有的值，那直接除以数量，就得到了平均值（mu）如果你没有所有值，可以利用（x-bar）估计population mean，x-bar是你既有的值算出来的平均值。

population variance，用你的data减去population mean（mu），平方后再除以样本数。

population std则是对population variance开根号。

然而，更多的情况是，你不可能直接算出来population mean，std，variance这些值，因为你只有有限的样本。

所以你得用x-bar代替mu，并将n-1代替n作为样本空间，计算variance，以及std。

因为我们算的是sample mean，而不是population mean，所以n需要减1。

为什么呢？请看下图

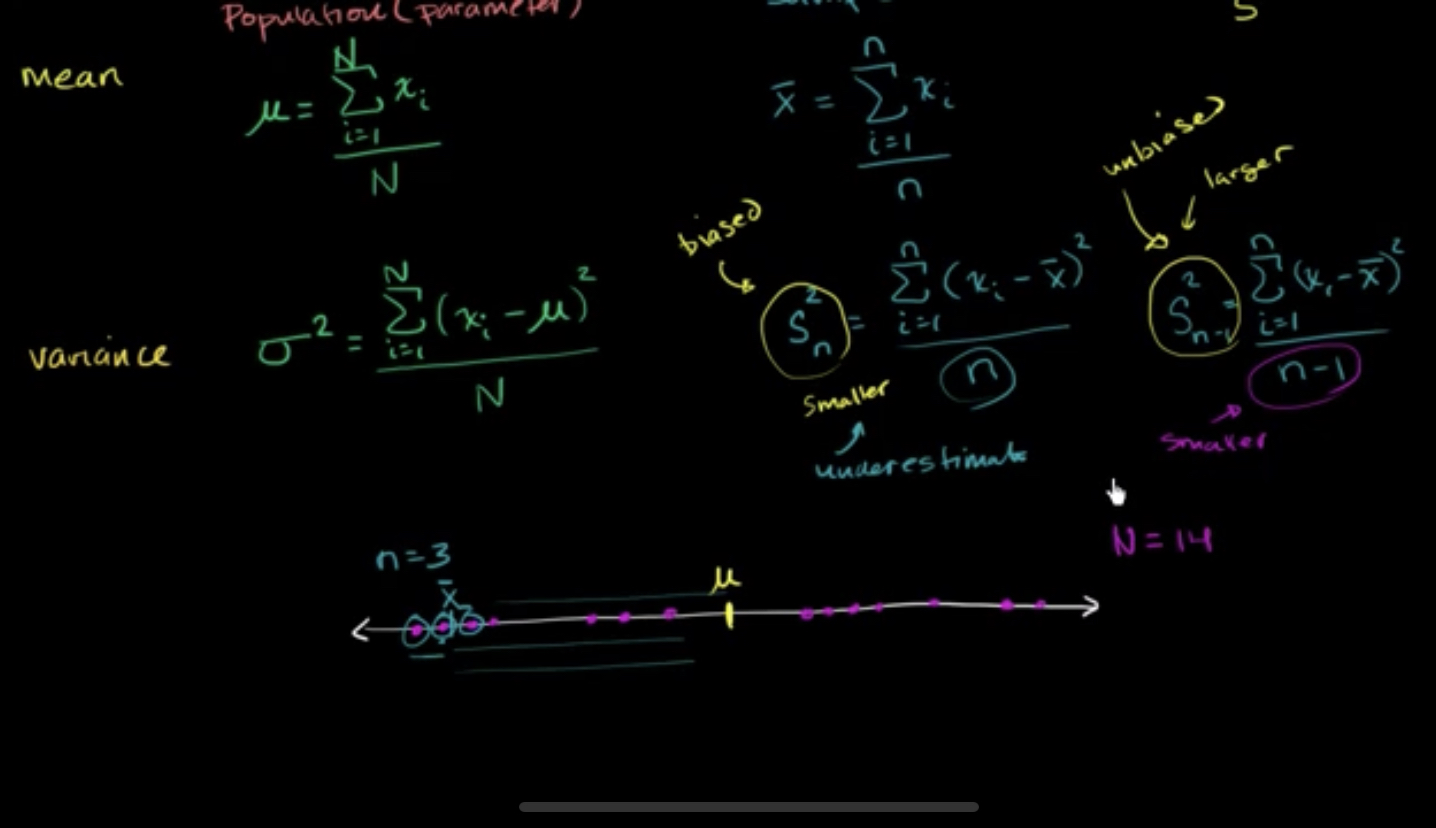
因为数据与sample mean之间的差值，要小于数据与population mean之间的差值。

6. What is a statistical model?

model，即模型。比如根据老鼠体重，预测体长，这就是一个 model.

在这个语境下，model是一种关系。

体重越大，体长越长。

有时候model中，x和y的关系，并不是一条直线。

model 可以很简单，也可以很复杂。

7. Sampling A Distribution

对一个分布进行抽样，假设你现在有一个随机的分布，我们可以从中抽样，来计算这个分布的mean值（x-bar）

你可以抽样很多次，于是你会得到一个mean值的分布，这个分布图像的mean，随着抽样的个数（sample size）的增加，抽样分布的mean，会趋向于真正的mean，即（population mean），抽样分布的图像，会接近正态分布，符合中心极限定理的定义。

这里的n增加，我们的图像的std会变小，即图像变得更窄，但更高。

Python 实践

1 2	import numpy as np import matplotlib.pyplot as plt

1	arr = np.random.randint(0,100,100)

Population parameters(actual)

1 2	# 用 Numpy 自带包计算 print("Population Mean: {} \nPopulation Variance:{}".format(np.mean(arr),np.var(arr)))

Population Mean: 50.29 
Population Variance:687.2659000000001

# 手动计算

# mean
population_mean = np.mean(arr)

# variance
value_squares = []

for num in arr:
    value = num - population_mean
    value_square = np.square(value)
    value_squares.append(value_square)
    
variance = np.sum(value_squares) / len(arr)

print("Population Mean: {} \nPopulation Variance:{}".format(population_mean,variance))

Population Mean: 50.29 
Population Variance:687.2659000000001

Samples parameters(estimate)

# sampling
sample = np.random.choice(arr,size=100)

# sample mean, x-bar
sample_x_bar = np.mean(sample)

# sample variance with numpy
sample_var = np.var(sample)

# sample variance by hand, n as denominator
absolute_values = []
for i in sample:
    absolute_value = i - np.mean(sample)
    absolute_value_square = np.square(absolute_value)
    absolute_values.append(absolute_value_square)

biased_variance = np.sum(absolute_values)/len(sample)
unbiased_variance = np.sum(absolute_values)/len(sample) - 1


print("Sample Mean:{}\nSample Variance:{}".format(sample_x_bar,sample_var))
print("\n")
print("Sample Variance Biased:{}".format(biased_variance))
print("Sample Variance Unbiased:{}".format(unbiased_variance))

Sample Mean:50.54
Sample Variance:726.8484


Sample Variance Biased:726.8484
Sample Variance Unbiased:725.8484

Sampling Distribution

x_bars = []

for i in range(100):
    # sampling
    sample = np.random.choice(arr,size=100)
    # sample mean, x-bar
    sample_x_bar = np.mean(sample)
    x_bars.append(sample_x_bar)

plt.hist(x_bars)
plt.show()

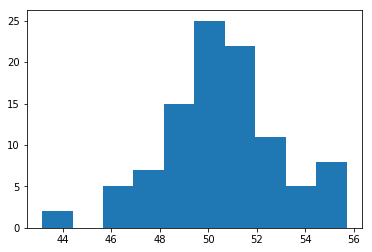
8. P-values

对于两个药物的测试结果如下，我们完全可以观察出，A药物明显有效果，而B无效，且无法断定说，这两者的表现，只是一种随机现象。

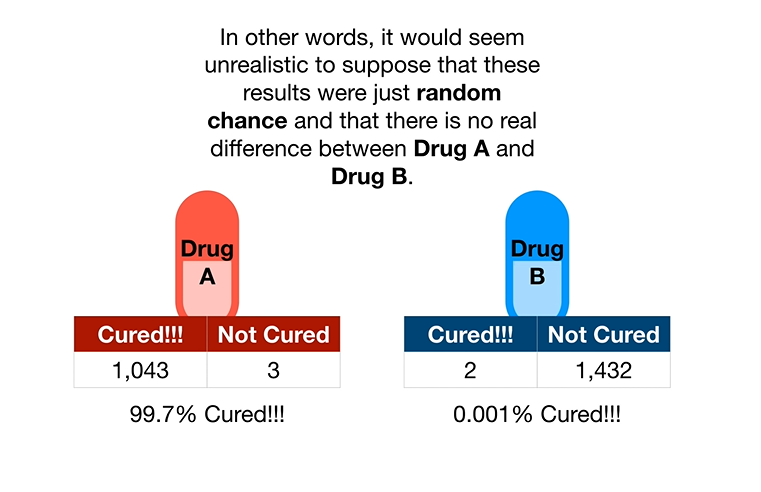
这时候就可以请p value发挥作用了。

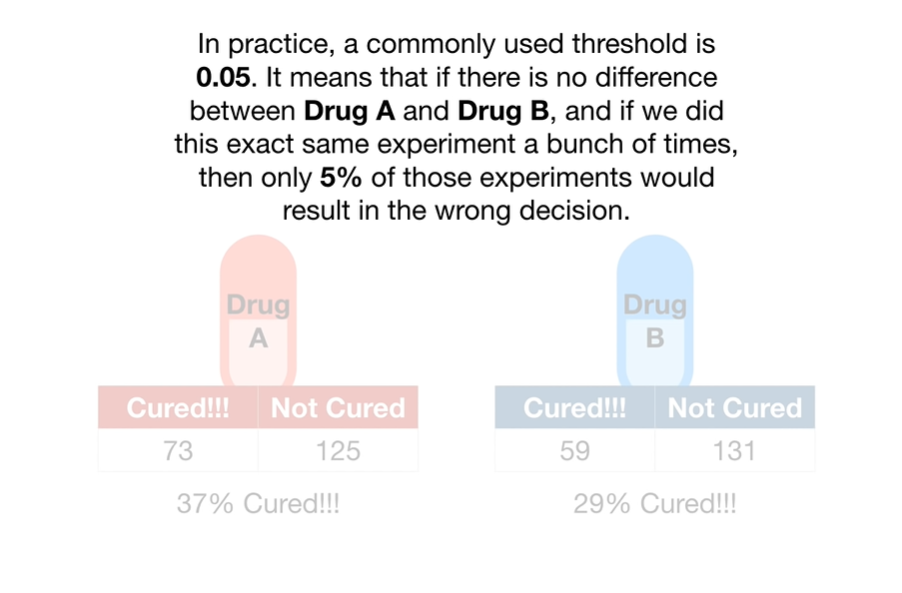
Calculate P-values

P-values有两种，One-Sided 和 Two-Sided。

我们一般谈后面那种，并避免使用第一种。

你扔了两次硬币，都是国徽面朝上，你觉得这个硬币应该是不正常的，你搞到了一个神奇硬币！

你想知道，这真的是一个神奇硬币吗？

于是你想验证，你假设，这个这个硬币和别的硬币没什么区别（Null Hypothesis）。

如果你接下，推翻了这个假设，即，这个硬币和别的是有区别的，那么你拿到的，就是神奇硬币了。

为了验证这个假设，我们来计算抛两次硬币的概率, 使用树形图来看，很明显，两枚硬币都是国徽面的概率是25%。

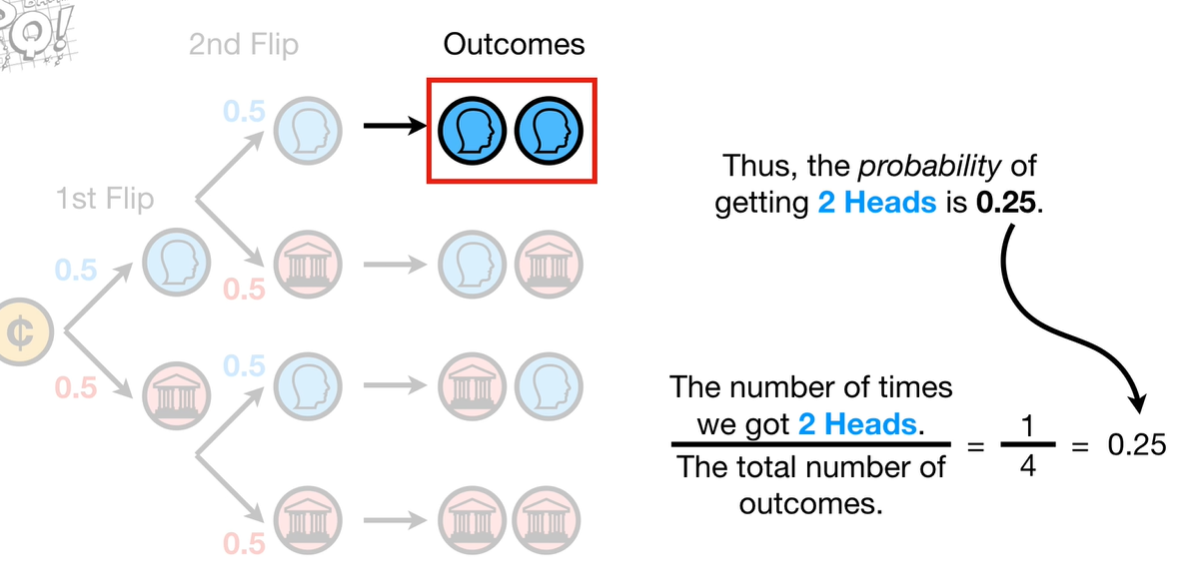
现在，我们再来算，我们得到两个人像面的p value,p-value 由 3 部分组成：

The probability random chance would result in the observation，在这里就是一个正常硬币，扔两次得到两次人像的概率，即0.25。
The probability of observing something else that is equally rare, 这里是两个人像或是两个国徽，也是0.25.
The probability of observing something rarer or more extreme. 这里是0，因为没有其他的结果比两个人像、两个国徽的概率更低。

现在，p-value 就是 0.25 + 0.25 + 0 = 0.5. 注意我们计算 p-value 的目的是测试假设：

我的硬币和其他硬币是一样的。

通常来说，当 p-value 小于0.05 的时候，我们会拒绝这个假设，但是现在的概率是0.5,所以这个假设是真的，也就是你拿到的，不是神奇硬币啦。

注意，得到两个人像面概率为0.25与得到两个人像面得p-value为0.25，这两者不一样。

为什么我们需要关心上面得条件2和3呢？

举个例子，当你送一朵花给你得意中人，你说：这是这个品种的花中最特别的。于是你得到了它的芳心。

但当她收到了10朵花，你说：这朵花和其余9朵花一样都很特殊。那这朵花，她也许就觉得不特别了，这是2的情况，所以我们把2的概率加进来。

也有可能是这样，你跟她说：还有很多的花，比现在这朵更稀有。她也会觉得这朵花不特别，这是3的情况。

现在我们知道扔2次，得到2个人像面的情况，如果扔5次得到4次人像呢？我们计算 p-value 看看(我们不关心顺序)：

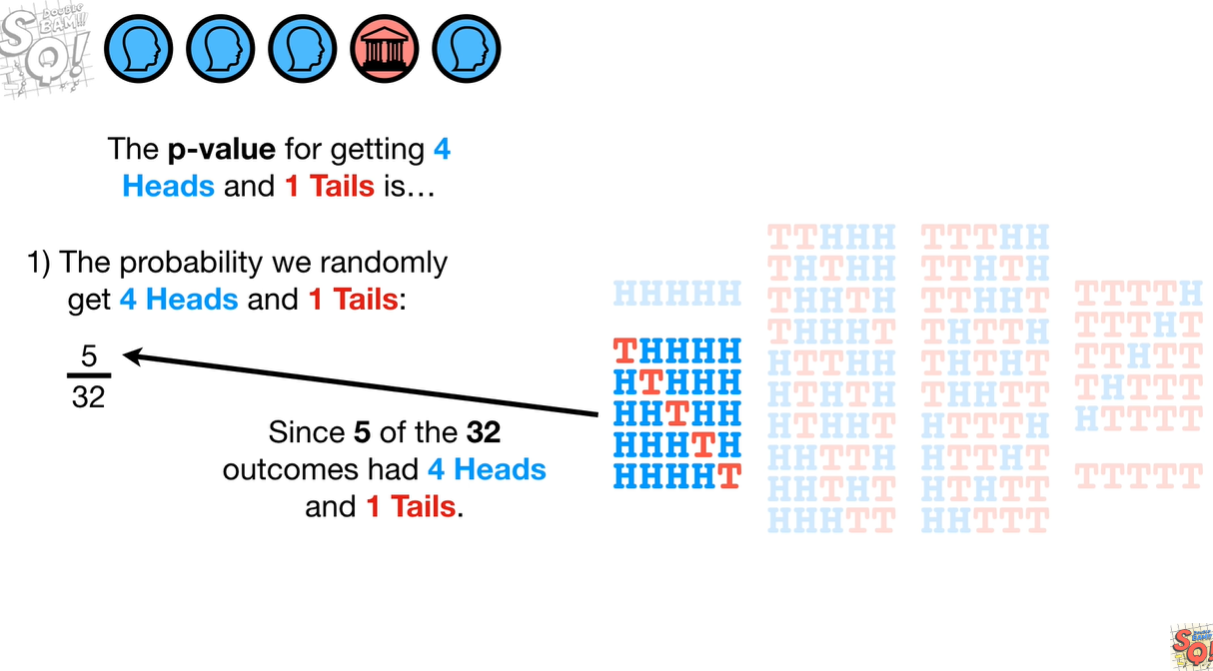
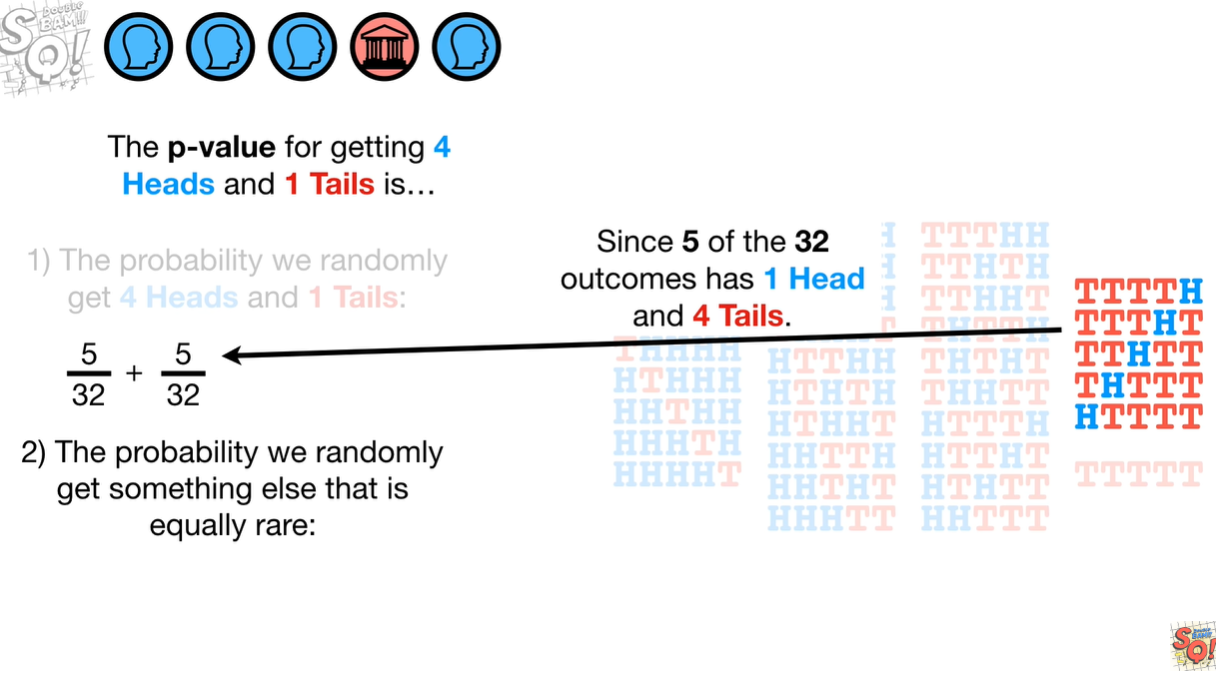
我们需要p-value小于0.05就可以拒绝这个假设了，但目前来看，好像还是无法拒绝:

对于连续的数据计算p-value，我们一般通过概率分布来计算，考虑一个身高的例子：

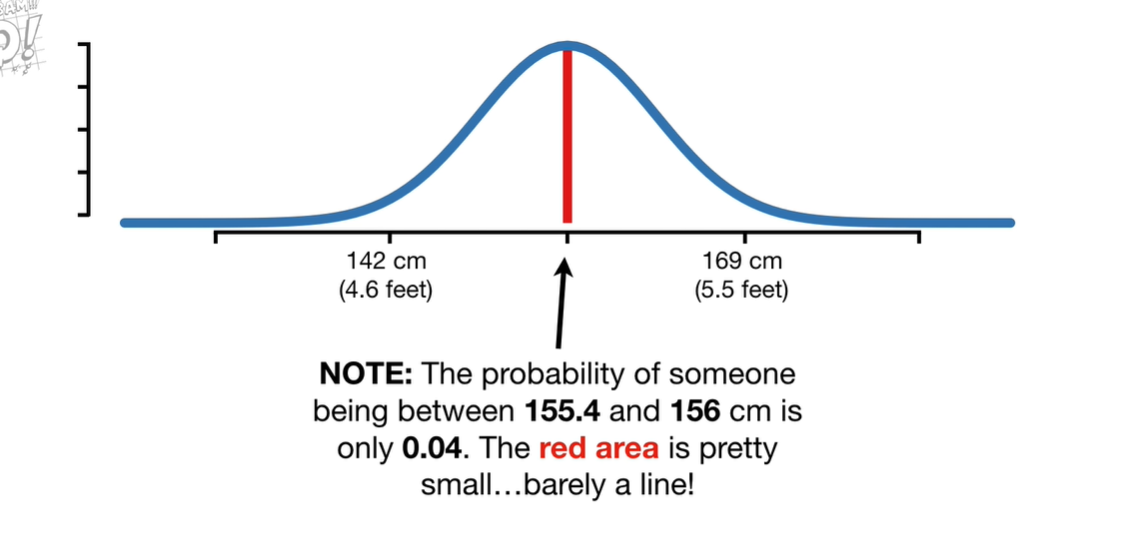
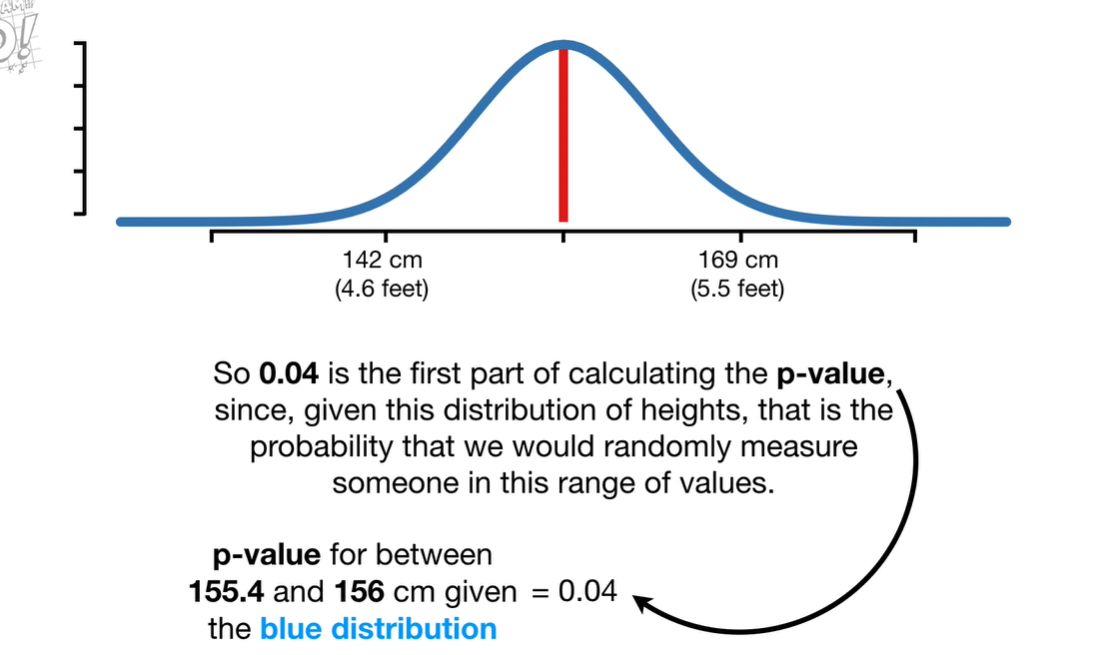
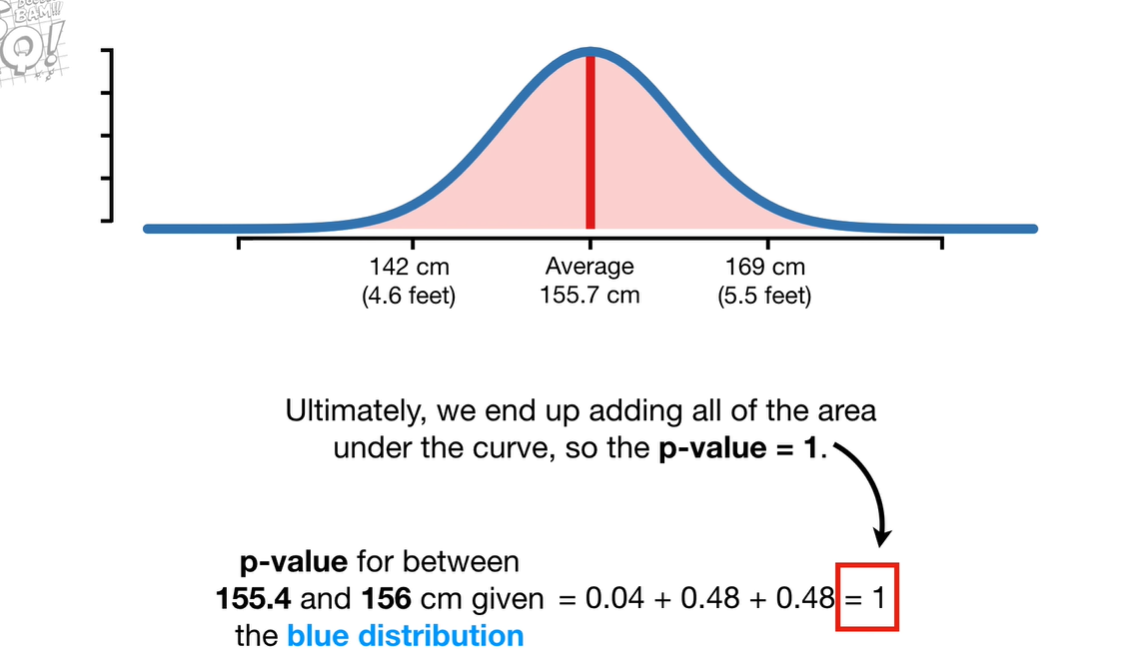
9. Covariance and Correlation

Covariance 一般可以分为三类，斜率为正的图像，斜率为负的图像，平行于x或y轴的图像。

即 positive trends, negative trends, no trends.

但 covariance 只能告诉你，数据是positive还是 negative 的trend，无法告诉你这个图像的slope，是陡峭还是平缓。

它也无法告诉你各个点与图像之间的距离。

如果所有的图像的 x或者y 值，是一样的，则 covariance 为0.

如果我们根据x和x本身来算 Covariance, 同时对比 2*x与 2*x 本身的图像，会发现两者的图像是一致的:

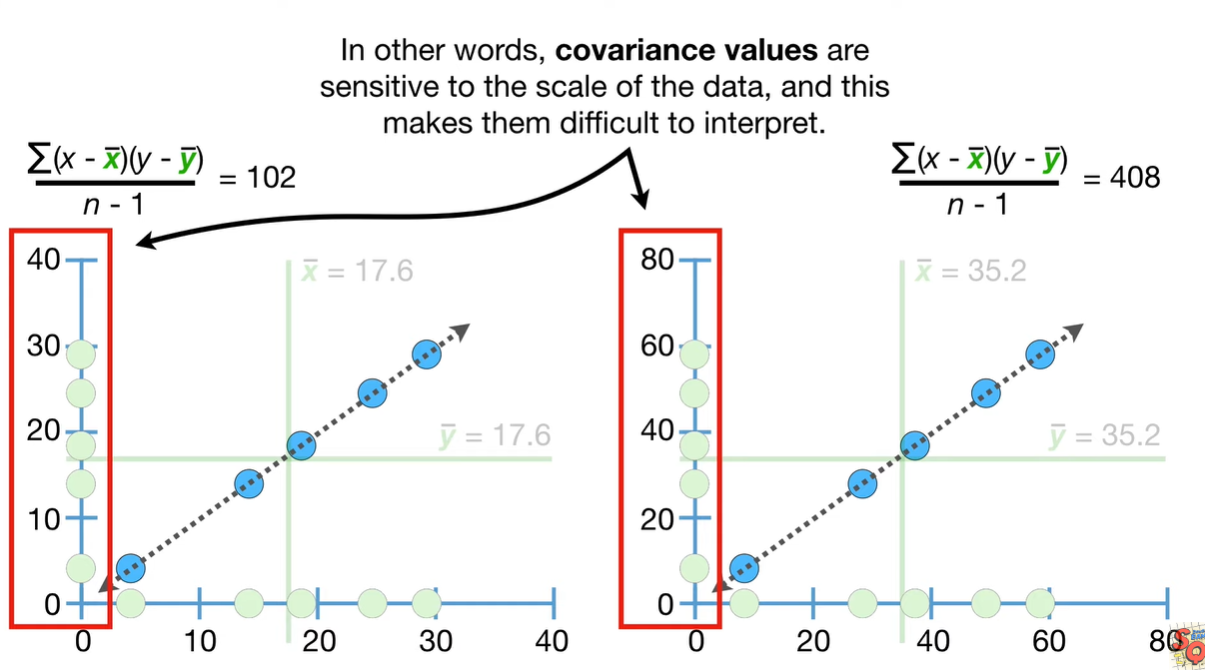
总的来说，Covariance 是根据各个点与平均值之间的距离来算的，这意味着它会受到点与均值之间距离的影响，也会受到坐标轴的影响。解决这个问题，引入下一个概念，即 Correlation。

10. R-squared

我们已经知道 Correlation 的概念。为什么需要 \(R^{2}\) 的概念，某些时候，它更容易解释，如 0.7 是 0.5 的两倍不容易理解，而0.7方是0.5方的两倍却很简单。

另外看一个老鼠的例子：

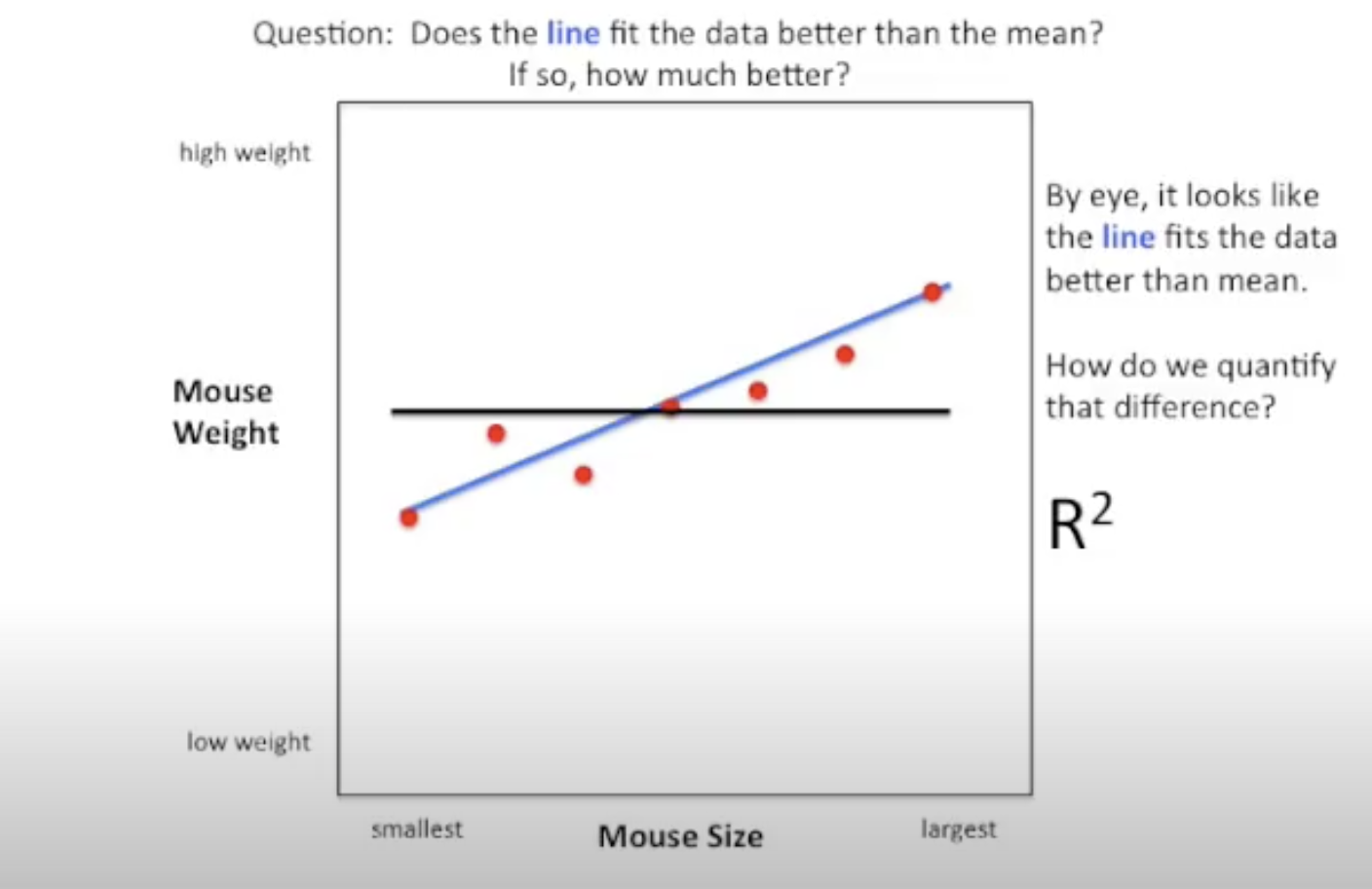
我们分别计算各点对于平均值（黑线）的方差，以及平均值对于fit的蓝线的方差，然后计算\(R^{2}\)。

公式为：

1	var(mean) - var(blue line) / var(mean)

结果是 81%, 这意味着蓝线比平均值小了81%的方差。

对于两个变量之间的关系来说，\(R^{2}\) 越高，说明拟合程度越好。

需要区别: \(R^{2}\) 和相关系数的关系。

11. Central Limit Theorem

中心极限定理，如果我们对0-1之间的数据抽样20个，计算mean，得出一个结果，然后绘制在另一个直方图上，如此反复几百遍后，我们得到的mean将会是一个正态分布的图。

这个原理，对于任何分布的图都适用。

摘录几则关于中心极限定理的话：

摘录来自: “赤裸裸的统计学。” Apple Books.

“中心极限定理是许多统计活动的“动力源泉”，这些活动存在着一个共同的特点，那就是使用样本对一个更大的数量对象进行推理”
“个大型样本的正确抽样与其所代表的群体存在相似关系。当然，每个样本之间肯定会存在差异（比如前往马拉松起点的这么多辆客车，每辆客车乘客的组成都不可能完全相同），但是任一样本与整体之间存在巨大差异的概率是较低的”
“如果我们掌握了某个正确抽取的样本的具体信息（平均数和标准差），就能对其所代表的群体做出令人惊讶的精确推理”
“如果我们掌握了某个样本的数据，以及某个群体的数据，就能推理出该样本是否就是该群体的样本之一”
“通过中心极限定理，我们就能计算出某个样本（客车上的肥胖乘客）属于某个群体（马拉松比赛选手）的概率是多少，如果概率非常低，那么我们就能自信满满地说该样本不属于该群体”
“如果我们已知两个样本的基本特性，就能推理出这两个样本是否取自同一个群体。”

那么，中心极限定理的实际意义是什么呢？

计算置信区间
t-test，即两个sample的mean是否不同
ANAVO,即三个sample或以上的mean是否不同

通常来说，为了中心极限定理的有效性，sample size必须要至少大于30.

12. Standard Deviation vs Standard Error

“标准差（Standard Deviation）是用来衡量群体中所有个体的离散性”，如心脏研究中所有参与者的体重分布”
“标准误差（Standard Error）衡量的仅仅是样本平均值的离散性。如果我们反复从弗雷明汉心脏研究数据库中抽取100名参与者作为样本，并计算其平均值，那么这些样本平均值的分布会是怎样一种情况？”

另外：

“标准误差就是所有样本平均值的标准差！”

“如果标准误差差很大，就意味着样本平均值在群体平均值周围分布得极为分散；如果标准误差差很小，就意味着样本平均值之间的聚集程度很高。”

关于这两者，还有一些图像上的规律：

“样本数量越多，其平均值就越不容易偏离整体平均值。图像也就越集中，因为大型样本受极端异常值的影响相对较小”
“数据分布越分散，那么其样本平均值的聚集程度就越低。”

其次，需要注意的是：

“如果标准差本身的数值很大，那么标准误差的数值也不会小。取自一个高度离散群体的大规模样本，其离散程度也会很高；与之对应，如果是一个高度聚集的群体，其样本围绕平均值的聚集程度也会很高。”

由于样本的平均值是正态分布的，即中心极限定理的内容，我们有以下的规律：

“差不多有68%的样本平均值会在群体平均值一个标准误差的范围之内，有95%的样本平均值会在群体平均值的两个标准误差的范围之内，有99.7%的样本平均值会在群体平均值3个标准误差的范围之内。”

Scott's Blog

统计基础概念

统计