Scott's Blog

学则不固, 知则不惑

0%

数据结构与算法参考

发表于 更新于 分类于 阅读次数： Valine：

系统的复习一下数据结构与算法的知识，包括 Python 实现的代码模板。

Update: 2021-8-22, 更新链表 python 实现

数组、链表、跳表

数组

申请数组，计算机在内存中给你开辟一段 连续 的地址。如果直接访问数组中的某个元素，不管是前后，时间复杂度是一样的 O(1).

问题：

  • 在中间位置插入元素，后面的元素都要移动，导致插入操作的时间复杂度不再是常数级的了，而是 O(n)，在最坏的情况下
  • 删除的时候，也一样，时间复杂度和插入一样

Java 数组实现

操作

  1. 判断数组的 Size 是否够
  2. 如果够，插入元素
  3. 如果不够，申请一个新的数组，size是当前的2倍，并将原来的数组拷贝到新的数组
  4. 将后面的元素往后挪

可见数组的操作中，存在大量的元素拷贝。

链表

在修改，添加，删除等操作频繁的情况下，数组并不好用，这时候推荐使用链表。链表的每一个元素都有 value 和 next，其中 next 指向下一个元素。这个元素一般使用 class 来定义，叫 node。

如果只有一个指针叫单链表，如果有两个双向的，叫双链表，头指针叫 head，尾指针叫 tail，如果 head 连接了 tail，叫循环链表。

Python 实现单链表，来自知乎，该文章还有关于双链表，循环列表的实现。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106

class Node(object):
    """单链表的结点"""

    def __init__(self, item):
        # item存放数据元素
        self.item = item
        # next是下一个节点的标识
        self.next = None

class SingleLinkList(object):
    """单链表"""

    def __init__(self):
        self._head = None

    def is_empty(self):
        """判断链表是否为空"""
        return self._head is None

    def length(self):
        """链表长度"""
        # 初始指针指向head
        cur = self._head
        count = 0
        # 指针指向None 表示到达尾部
        while cur is not None:
            count += 1
            # 指针下移
            cur = cur.next
        return count

    def items(self):
        """遍历链表"""
        # 获取head指针
        cur = self._head
        # 循环遍历
        while cur is not None:
            # 返回生成器
            yield cur.item
            # 指针下移
            cur = cur.next

    def add(self, item):
        """向链表头部添加元素"""
        node = Node(item)
        # 新结点指针指向原头部结点
        node.next = self._head
        # 头部结点指针修改为新结点
        self._head = node

    def append(self, item):
        """尾部添加元素"""
        node = Node(item)
        # 先判断是否为空链表
        if self.is_empty():
            # 空链表，_head 指向新结点
            self._head = node
        else:
            # 不是空链表，则找到尾部，将尾部next结点指向新结点
            cur = self._head
            while cur.next is not None:
                cur = cur.next
            cur.next = node

    def insert(self, index, item):
        """指定位置插入元素"""
        # 指定位置在第一个元素之前，在头部插入
        if index <= 0:
            self.add(item)
        # 指定位置超过尾部，在尾部插入
        elif index > (self.length() - 1):
            self.append(item)
        else:
            # 创建元素结点
            node = Node(item)
            cur = self._head
            # 循环到需要插入的位置
            for i in range(index - 1):
                cur = cur.next
            node.next = cur.next
            cur.next = node

    def remove(self, item):
        """删除节点"""
        cur = self._head
        pre = None
        while cur is not None:
            # 找到指定元素
            if cur.item == item:
                # 如果第一个就是删除的节点
                if not pre:
                    # 将头指针指向头节点的后一个节点
                    self._head = cur.next
                else:
                    # 将删除位置前一个节点的next指向删除位置的后一个节点
                    pre.next = cur.next
                return True
            else:
                # 继续按链表后移节点
                pre = cur
                cur = cur.next

    def find(self, item):
        """查找元素是否存在"""
        return item in self.items()

链表复杂度

操作

  1. 将插入位置前的元素的next指向新节点，新节点的指向后节点，操作两次，常数级别，O(1)
  2. 与插入类似

优点：

  • 不用群移，不需要复制元素
  • 移动，修改的效率很高

缺点

  • 访问中间节点，必须一步一步往后挪，所以复杂度为O(n)

跳表

image.png
  • 弥补链表的设计缺陷而设计，为了加速链表访问的速度，在节点之间搭建快速路（索引）。
  • 索引越多，速度越快，但是也没有降到O(1)，而是 O(logn)
  • 现实中，因为索引经常操作，维护成本较高
  • 空间复杂度为 O(n)，但肯定还是比链表高

栈、队列

  • 栈相当于一个瓶子，先放进去的后面才能拿出来。

  • 队列相当于一个管子，先放进去的先出来。

这两个，复杂度添加删除都是 O(1)，查询则是 O(n)，因为它们内部元素是无序的，查任何元素都需要遍历整个数据结构。

实战中，其实纯粹的栈、队列用的很少，更多的用的是双端队列(Double-End queue)，一个栈和队列的结合体，它两边都可以 push，pop，复杂度和正常的栈、队列都一样。

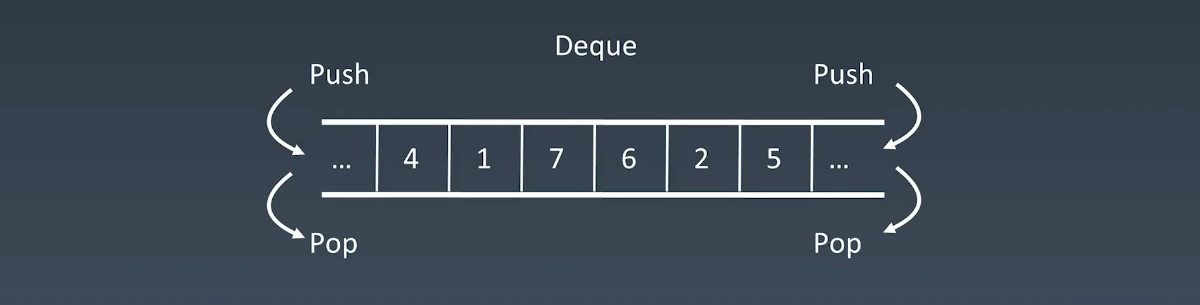
image.png

栈的一些操作，可以直接通过 python 中的列表实现

1
2
3
4
list = []
list.append() == push
list.pop() == pop
list[-1] == peek

优先队列

也就是元素是有优先级的，它的插入是 O(1), 取出操作 O(logN), 因为需要按照元素的优先级取出。底层的实现方式较为多样和负责，有 heap, bst, treap.

哈希表、映射、集合

哈希表也叫散列表，现实中用的比较多，类似字典的key value对，但它是通过哈希函数建立一个映射关系，key 相当于关键码值，value 也就是存放数据的地方叫哈希表。

现实中一般应用在电话号码，用户信息表，缓存，键值对存储（Redis）。

哈希函数有很多种，选的好可以让生成的地址比较分散，不会重复，这里重复的意思就是，比如我字符 scott 生成的地址是 9，然后 zhang 生成的也是9，这就重复了，这叫哈希碰撞。

但发生了碰撞怎么办呢？可以在相同得位置，拉出一个链表出来，把信息存在这个链表上，如果哈希函数选的不好，链表很长，复杂度会变成O(n)，而没有链表得情况下是 O(1)。

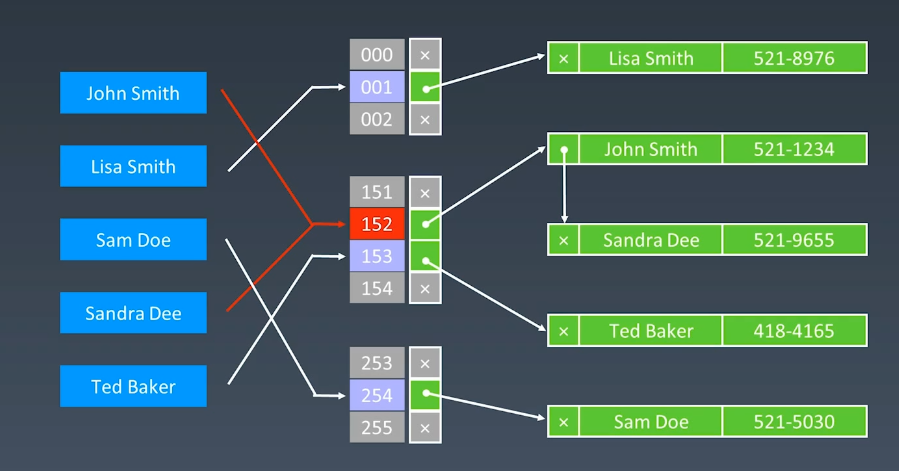
发生哈希碰撞后的哈希表
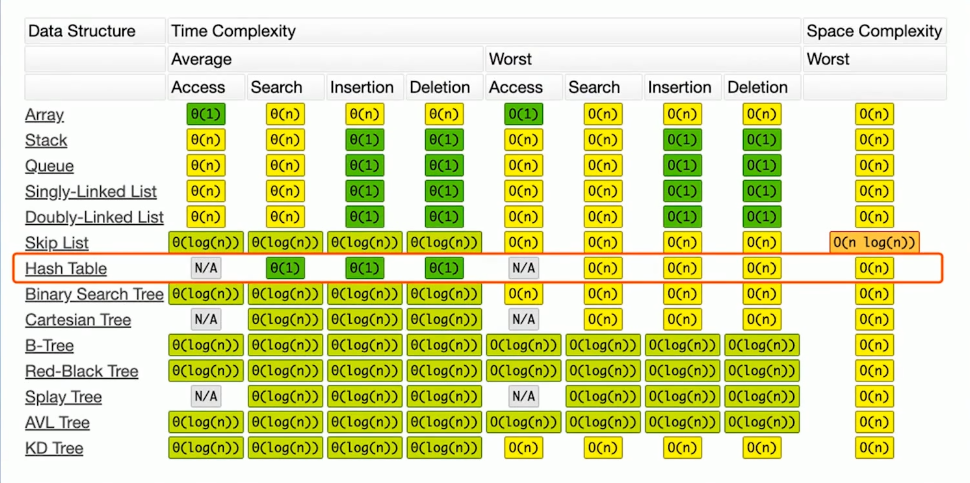
哈希表的复杂度

哈希表在 python 中有两种，Dictionary 和 Set，在 Java 中，可能只是一个接口，比如 Set 的实现有很多种，有基于红黑树的，基于二叉树的等等。

树、二叉树、二叉搜索树

2 维数据结构。

树

树的示意图

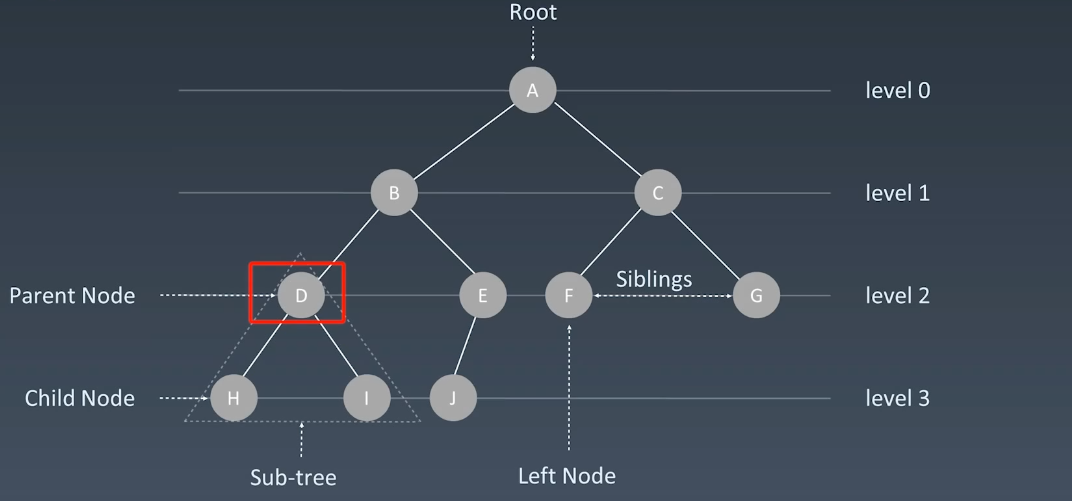
image.png

为什么会出现树呢？工程实践就是二维的,树和链表没有本质上的区别，只是从1维到了二维。。树的遍历怎么办？对于一维数组，你可以直接循环遍历，而对于树，则有好几种方式：

  1. 前序 (Pre-order)：根，左边，右边
  2. 中序 (In-order)：左边，根，右边
  3. 后序 (Post-order)：左边，右边，根

二叉树

二叉树，也就是儿子节点只有两个。

image.png

二叉搜索树 BST

如果树要查找元素，就必须要遍历，如果树里的元素没有顺序，那和列表什么的没区别。于是为了方便搜索，我们对树进行了排序，定义了二叉搜索树，它的特点是一颗空树或者具有以下性质的二叉树：

  1. 左子树上所有节点的值均小于根节点的值；
  2. 右子树上所有节点的值均大于它的根节点的值；
  3. 以此类推：左右子树也分别为二叉查找树（重复性）
  4. 至多只有两个儿子节点（Left和Right）

它的查找非常方便：

  • 当前节点值 == 查找的值，查找结束，返回；
  • 当前节点值大于查找的值，则进入左子树；
  • 当前节点值小于查找的值，则进入右子树；

对它进行中序遍历，得到的结果就是升序排列后的；

排序后的树，查询和操作都是 logn 的复杂度，将当前节点与查询的节点做比较，每次可以筛掉一般的值，所以变成logn，虽然不是 O(1)，但logn 还是比 n 是不知道快多少了。但是，在极端情况下，B树会退化成一棵线性树,此时，B树的查找、新增、删除时间复杂度都是 O(n) = N。

这时候可以对节点之间的高度作出规定，比如对于一个现有的二叉搜索树，要求它的左右节点高度差小于1，这时候它就变成了一颗平衡二叉树（AVL），这部分将在后面介绍。

看二叉搜索树的查询动画，see also Visualgo.

二叉树的遍历，树的循环，效率是比较麻烦的，反倒是写递归比较简单，树的各种操作，不要害怕递归。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# 使用递归
class Solution:
    def __init__(self):
        self.traverse_path = []

    # 中序遍历
    def inorder(self, root):
        if root:
            self.inorder(root.left)
            self.traverse_path.append(root.val)
            self.inorder(root.right)

        return self.traverse_path

    # 前序遍历
    def preorder(self, root):
        if root:
            self.traverse_path.append(root.val)
            self.preorder(root.left)
            self.preorder(self.right)

    # 后序遍历
    def postorder(self, root):
        if root:
            self.postorder(root.left)
            self.postorder(root.right)
            self.traverse_path.append(root.val)

也可以使用循环来遍历二叉树，下面举一个中序遍历的例子。

这个算法需要一个栈和数组；栈保存需要处理的节点，数组保存结果；

使用 curr 指针遍历这个树，第一步从 根节点开始，找最左边的节点，并将中间遇到的节点放到栈中以备使用。当一个节点没有左节点存在的时候（它此时在栈中），说明到了最左边的节点。将这个节点从栈中取出放到数组，然后还需要检查这个节点是否有右节点（刚才只确认了这个节点没有左节点，如果有的话，还需要将它的右节点放入栈中）

同时，根据中序遍历的特性，将最左边节点的父节点放到数组中，然后检查这个父节点是否有右节点，如果有，放入栈中，如果没有则继续处理栈顶元素，即将其放入数组，然后检查是否有右节点最后返回数组。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def inorderTraversall(root):
    if not root:
        return []

    res, stack = list(), list()
    current = root

    # 开始循环，结束的条件是 current 为空，或者栈为空
    while current or len(stack):
        while current:
            current = current.left
        # 取栈顶的第一个节点，即找到的最左边节点，放入数组
        node = stack.pop()
        res.append(node)
        # 检查该节点是否有右节点
        # 将右节点直接给 current ，如果没有右节点，则 current 为空
        # 那么会直接处理栈顶的节点，即父节点
        current = node.right
    return res

图

图又是什么呢？图就是上面的节点中，子节点又连接到兄弟节点甚至是父节点去了。

Linked List 是特殊化的 Tree，Tree是特殊化的 Graph.

递归

递归本质上类似与循环，即通过循环调用自己，以前使用的汇编语言，那时候没有循环嵌套这么一说，更多的时候就是你之前的指令写在上面地方，就不断的调用，从汇编的角度看，其实汇编的代码里，循环和递归差不多。

递归的特点，类似于盗梦空间。

  • 向下进入梦境，向上回到原来那层，只能一层一层进入或者退出。
  • 每一层的环境和周围的人都是一份拷贝
  • 通过声音返回上一层（return）
1
2
3
4
def Factorial(n):
    if n<=1:
        return 1
    return n*Factorial(n-1)
执行逻辑

递归代码模板：

1
2
3
4
5
6
7
8
9
10
11
12
13
def recursion(level, param1, param2, ...):
	# recursion terminator 终结条件
	if level > max_level:
		process_result
		return

    # process logic in current level 处理当前层的逻辑
    process(level, data...)

    # drill down 下探到下一层，带上参数
    self.recursion(level+1, p1, ...)

    # reverse the current level states if needed 如果需要递归完了清理当前层

思维要点：

  • 不要人肉递归
  • 找到最近，最简的方法，拆解成可重复解决的问题（最近重复子问题）
  • 数学归纳法的思维

分治、回溯

递归里面的细分类

碰到一个题目，我们要去找重复性，重复性有两种：

  • 最近重复性 -> 分支、回溯，递归
  • 最优重复性 -> 动态规划

分治

大问题都是子问题、复杂问题构成的，解决问题本质上就是找重复性，分解问题，组合子问题的结果。

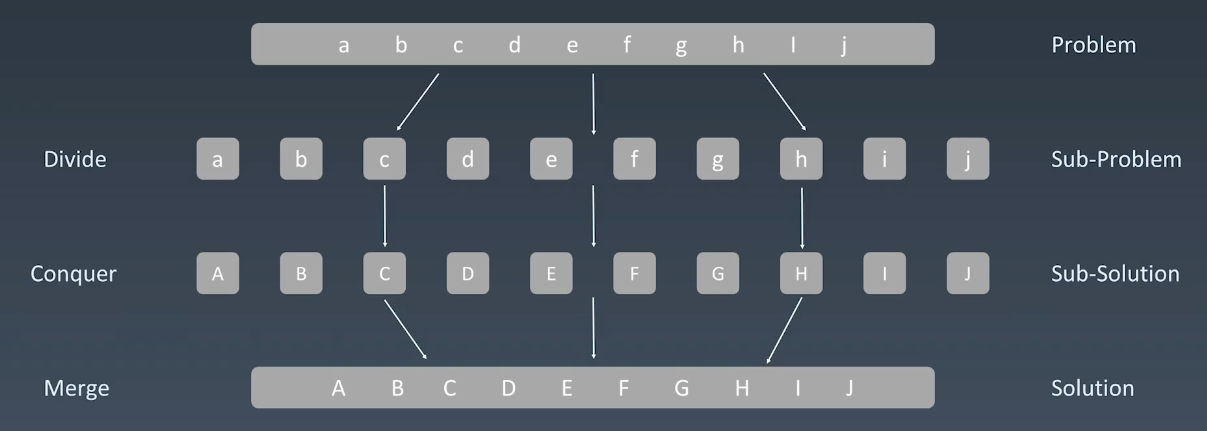
image.png

分治的代码模板:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def divide_conquer(problem, param1, param2, ...):
    # recursion terminator
    if problem is None:
        print_result
        return
   	# prepare data
    data = prepare_data(problem)
    subproblems = split_problem(problem, data)
    # conquer subproblems
    subresult1 = self.divide_conquer(subproblems[0], p1, ...)
    subresult2 = self.divide_conquer(subproblems[1], p1, ...)
    subresult3 = self.divide_conquer(subproblems[2], p1, ...)
    ...
    # process and generate the final result
    result = process_result(subresult1, subresult2, subresult3)
    # revert the current level states

回溯

采用试错的思想，分步解决一个问题，如果分布方案不解决问题，会取消上一步或几步的计算，再通过其他可能的分步方案寻找答案。

简单来说就是，每一层我都有不同的办法，一个一个试。

深度优先、广度优先搜索

深度优先

1
2
3
4
5
# 树的定义
class TreeNode
	def __init__(self, val):
        self.val = val
        self.left, self.right = None, None

深度优先就是先往最深处的节点走，发现没有子节点了，返回到有子节点的节点，继续往下面走。

示例代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# 非递归实现
def DFS(self, tree):
	if tree.root is None:
		return []
	visited, stack = [], [tree.root]

    while stack:
        node = stack.pop()
        visited.add(node)

        process(node)
        nodes = generate_related_nodes(node)
        stack.push(nodes)

# 递归
def dfs(node, visited):
	# terminator
	if node in visited:
		return
	# already visited
	visited.add(node)
	# process current node here
	for next_node in node.children():
		if not next_node in visited:
			dfs(next_node, visited)

广度优先

广度优先遍历，类似与一个水滴滴到根节点，然后像水波一样一层一层扩散下去，这种思想在算最短路径的时候，比深度优先效率高。遍历的方式使用队列实现

1
2
3
4
5
6
7
8
9
10
11
12
13
def BFS(graph, start, end):
    queue = []
    queue.append([start])
    visited.add(start)
    while queue:
        node = queue.pop()
        visited.add(node)

        process(node)
        nodes = generate_related_nodes(node)
        queue.push(nodes)
     # othres processing work
     ...

这里的算法为了方便理解，举个例子，就好像要访问公司的人员信息，首先先看老总的信息，老总看完了，放到 visited 数组，然后看他有没有其他下属，有的话全部取出来放到队列（先进先出）

贪心算法

贪心算法在每一步选择中，都采取当前状态下最好或最优的选择，从而导致结果是最好的或最优的算法。（有一定的局限性，因为当下最优不一定全局最优）

动态规划会保存以前的运算结果，并根据以前的结果对当前进行选择，有回退功能。

贪心法主要解决一些最优化问题，图中的最小生成树，求哈夫曼编码等。

一旦一个问题可以通过贪心算法解决，那么贪心法一般是解决这个问题的最好办法。

适用于贪心的情况，即问题可以分解成子问题，子问题的最优解可以递推到最终问题的最优解

二分查找

一定记住二分查找的前提（肌肉记忆）:

  1. 目标函数单调性（单调递增或递减），才可以通过特征排除掉前半部分或后半部分
  2. 存在上下界（bounded），没有上下界，空间可能无限大
  3. 能够通过索引访问（index acccessible)，如果是单链表，即使有序，也比较难
1
2
3
4
5
6
7
8
9
10
11
# 假设数组是有序的
left, right = 0, len(array)-1
while left < right:
    mid = (left + right) /2
    if array[mid] == target:
        # find the target!
        break or return
   	elif array[mid] < target:
        left = mid + 1
    else:
        right = mid -1

动态规划

  • Dynamic Programming（一种解决问题的办法）, 本质就是将复杂问题，分解成小问题，可以理解为动态的递推，每一步保存最优解，淘汰掉那些不怎么好的，然后最终求得总体的最优解。
  • 直接递归的复杂度是指数级的，如果淘汰掉一些解，可以变成 n 平方

字典树

字典树的数据结构

之前我们的树，内部就是值本身，而是把字符串拆成单个得字幕存储。

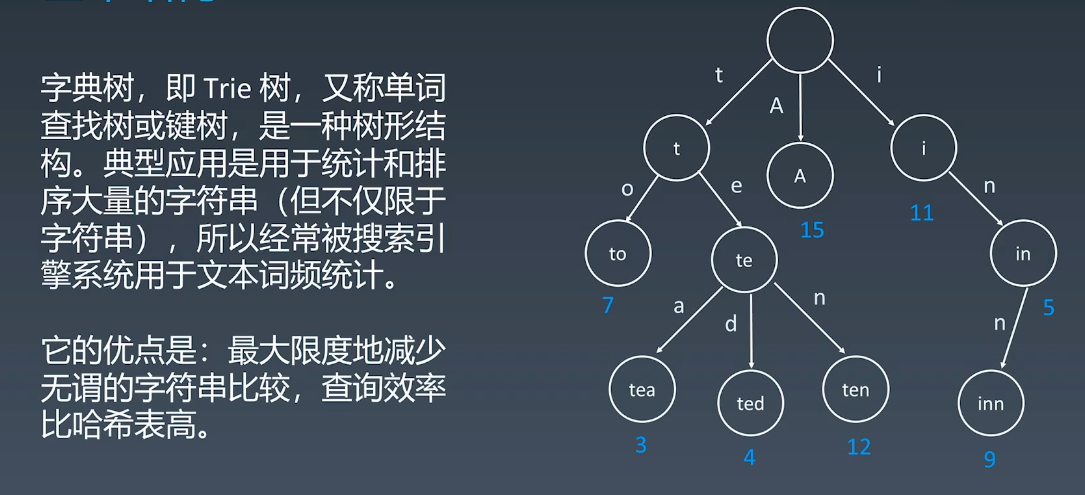
image.png
  • 节点本身不存完整单词
  • 根节点到某一结点，连起来即为单词
  • 每个不同的边都是不一样的字符

这种结构中，节点还可以存储其他信息，比如这个节点所得到的单词出现的频次。这种结构的核心思想是空间换时间。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Trie(object):
    def __init__(self):
        self.root = {}
        self.end_of_word = "#"

    def insert(self, word):
        node = self.root
        for char in word:
            node = node.setdefault(char, {})
        node[self.end_of_word] = self.end_of_word

    def search(self, word):
        node = self.root
        for char in word:
            if char not in node:
                return False
           	node = node[char]
        return self.end_of_word in node

    def startsWith(self, prefix):
        node = self.root
        for char in prefix:
            if char not in node:
                return False
            node = node[char]
         return True

并查集

属于一种比较跳跃式的数据结构，如果你会就很简单，如果不会就很难，它使用情景主要是在组团、配对问题。

这两个个体是不是在一个集合之中。

基本操作

  • makeSets(s): 新建并查集，其中包括s个单元素集合。

  • unionSet(x, y): 集合合并，要求不相交才合并

  • find(x): 判断 x 所在集合的代表

每个元素都有一个 parent 数组指向自己，表示自己是自己的集合。

合并

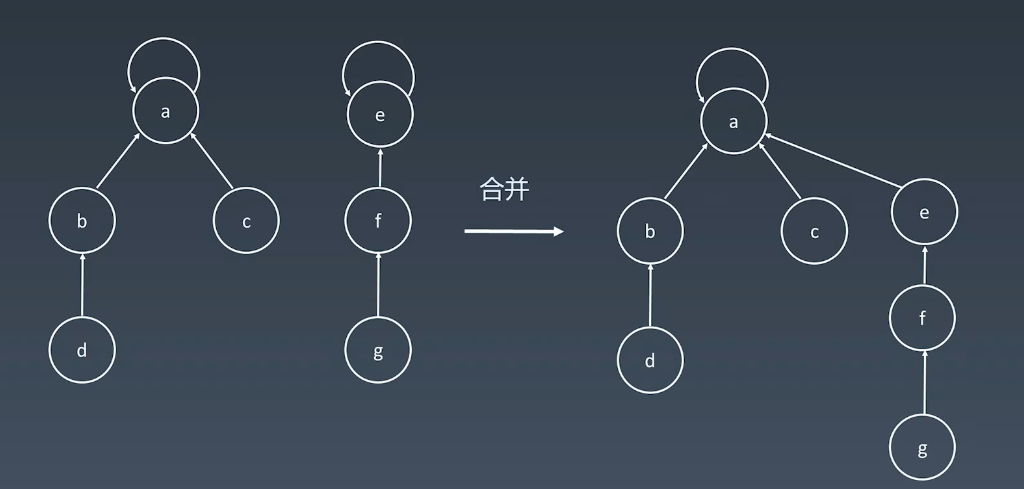
image.png

路径优化

image.png

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def init(p):
    p = []i for i in range(n)

def union(self, p, i, j):
    p1 = self.parent(p, i)
    p2 = self.parent(p, j)
    p[p1] = p2

def parent(self, p, i):
    root = i
    while p[root] != root:
        root = p[root]
    while p[i] != i:
        x = i
        i = p[i]
        p[x] = root
    return root

高级搜索

剪枝

说高级搜索前，什么是初级搜索呢？

  1. 朴素搜索

  2. 优化方式：不重复、剪枝，剪枝就是在搜索的时候去掉重复，或者剪去是一些没必要的访问

  3. 搜索方向

    1. DFS，深度优先，没有优先级，傻搜

    2. BFS，广度优先

搜索的话可以通过双向搜索，启发式搜索来优化。

image.png

双向BFS

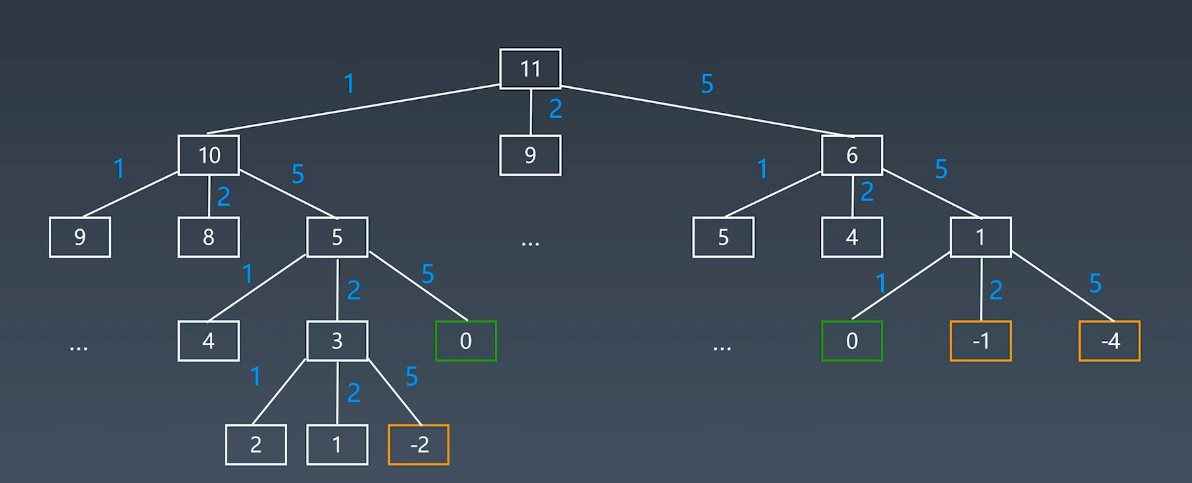
问题：找出A到L的最短路径

image.png

这种需求，我们一般使用广度优先算法，而双向 BFS 的意思是，从两边一起进行广度优先算法的遍历，两边一起逼近中间，这样就可以提高效率。

1
![image.png](https://i.loli.net/2021/08/14/J3fKMgXRkuynHOd.png)

启发式搜索 Heuristic Search (A*)

只能搜索，根据某项条件，我们去优化条件，也可以理解为思考型搜索，本质上是用优先级。

这里就要用到优先队列了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def AstarSearch(graph, start, end):
    pq = collections.priority_queue() # 优先级，估价函数
    pq.append([start])
    visited.add(start)

    while pq:
        node = pq.pop()  # 能更智能一点吗？
        visited.add(node)

        process(node)
        nodes = generate_related_nodes(node)  # 正常的BFS代码

        unvisited=[node for node in nodes if node not in visited]
        pq.push(unvisited)

这里怎么来定优先级呢？这就需要你按照对题目的理解把估价函数写出来。

AVL和红黑树

二三树，B树，B+树，B-树。

如何保持一棵树的平衡？

AVL

  1. Balance Factor，因为二叉树的查找只与高度有关，平衡因子是它的左子树的高度减去右子树的高度（有时候相反）,balance factor = {-1, 0, 1}
  2. 通过旋转操作来进行平衡（四种）

那么如何判断高度呢?

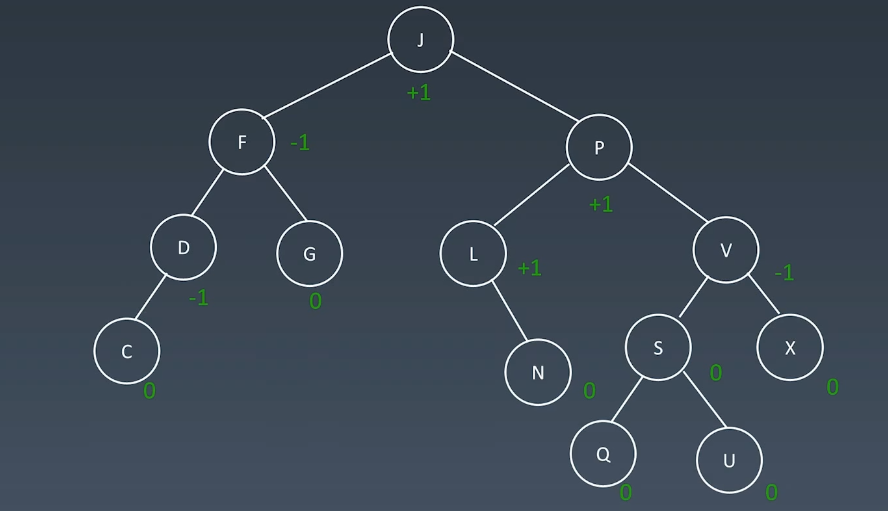
image.png

通过高度的值不超过1，不小于-1来判断一棵树是否需要调整，即旋转，旋转的方式有：

  1. 左旋
  2. 右选
  3. 左右旋
  4. 右左旋

缺点：需要额外的信息存储，且调整次数频繁。

红黑树

也是一种近似平衡的二叉搜索树，它能确保任何一个节点的左右子树高度差小于两倍，具体来说：

  • 每个节点要么是红色，要么是黑色
  • 根节点是黑色
  • 每个叶节点（NIL节点，空节点）是黑色的。
  • 不能有相邻接的两个红色节点
  • 从任何一个节点到每个叶子的所有路径都包含相同数目的黑色节点

这些性质就让红黑树的时间复杂度可以保持在 logn 的水平，不会退化，需要调整的时间也是相对比较折中。

下面是 AVL 与 红黑树的对比：

image.png
  • 如果读操作非常多写操作少就用 AVL，它插入、删除需要的操作比较多。
  • 插入操作也很多，或者操作、查询需求差不多，就用红黑树

位运算

位运算简单说就是进制转换，比如十进制转二进制，在进制表示中，4(d) 中的 d 表示的是十进制，0100 中零开头表示2进制。

具体转换的算法可以参考这里。

位运算符

含义 运算符 示例
左移 << 0011 => 0110
右移 >> 0110 => 0011
按位或，有1则1 | 0011 | 1011 => 1011
按位与，有0则0 & 0011 & 1011 => 0011
按位取反，0变1，1变0 ~ 0011 => 1100
按位异或，相同0不同1 ^ 0011 ^ 1011 => 1000

异或特点

异或操作的一些特点：

  • x^0 = x, 只要 x 和 0 相同的就为 0，不同的为 1，所以这里 x^0 就等于 x
  • x^1s = ~x, 1s 指的是全1，也就是等于0取反 ~
  • x^(~x)=1s, 取反后，所有位置都不一样，所有都不同，都是1，1s
  • x^x=0, 异或相同为0，所有都是0
  • c=a^b ,a^c=b 则 b^c=a, 交换两数
  • a^b^c = a^(b^c) = (a^b)^c, associative

指定位置的位运算

image.png

实战运算要点

image.png

布隆过滤器，LRU Cache

布隆过滤器

在说布隆过滤器之前，回顾一下哈希表，前面说过哈希表在哈希操作的时候，有可能会得到一样的地址（整数），这时候会采用拉链的办法，也就是在同样的地址上叠罗汉。

在哈希表的应用中，我们发现，有时候我们并不需要去存储元素的信息本身，而是只需要知道某个信息在我们的表中有没有。

如果我们只是需要知道某个信息在表里有没有，这时候 Bloom filter 就设计出来了。

布隆过滤器具 vs 哈希表

  • 空间效率和查询时间都远远超过一般算法
  • 缺点是有一定的误识别率和删除困难

布隆过滤器具原理

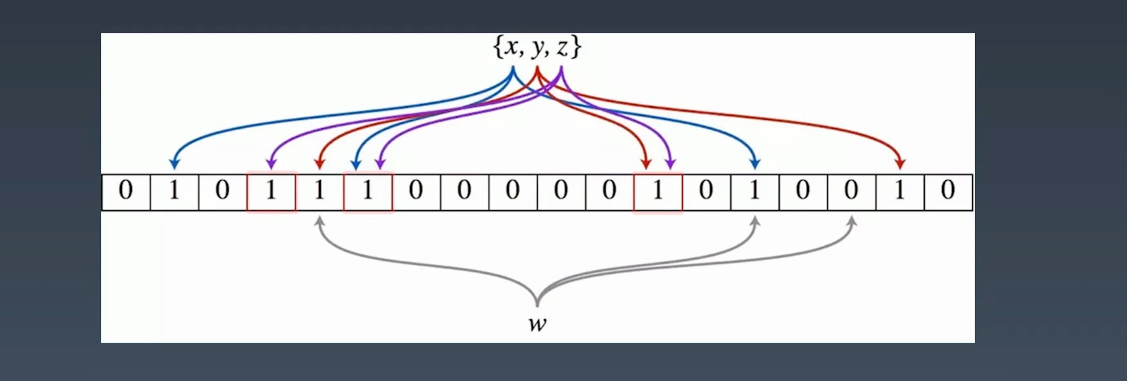
image.png

现在有 xyz 三个元素需要存储，布隆过滤器会对每一个元素执行哈希，得到一组值，然后再将这组值插入到下面的框框中，y 和 z 也是同理，这样下次查询的时候，只需要查看这些对应的位置是否为1就好了，而且查询的时候，我只需要判断任意一个元素是0，那么就可以判断这个元素是不在这个表中的。

但是这种查法可能会有问题，比如下面的这个B：

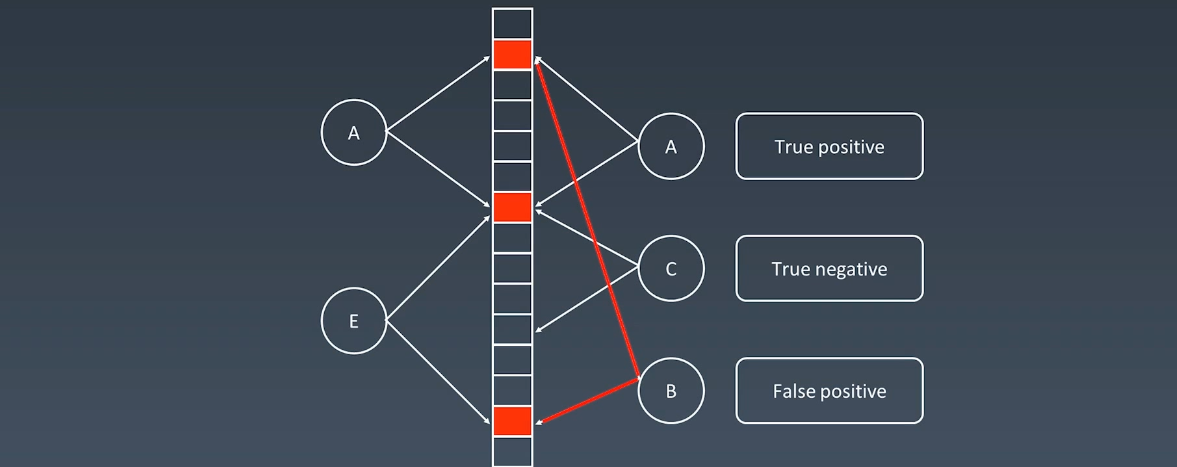
image.png

对于一个元素，布隆过滤器可以确定一个元素不存在，但只可以说某个元素有可能存在。

布隆过滤器一般放在数据库的外层当作缓存使用。

布隆过滤器具案例

  1. 比特币网络
  2. 分布式系统（Map-Reduce）- Hadooop，search engine
  3. Redis 缓存
  4. 垃圾邮件、评论等的过滤

布隆过滤器具 Python实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
bfrom bitarray import bitarray
import mmh3

class BloomFilter:
    def __init__(self, size, hash_num):
        self.size = size
        self.hash_num = hash_num
        self.bit_array = bitarray(size)
        self.bit_array.setall(0)

    def add(self, s):
        for seed in range(self.hash_num):
            result = mmh3.hash(s, seed) % self.size
            self.bit_array[result] = 1
    def lookup(self, s):
        for seed in range(self.hash_num):
            result = mmh3.hash(s, seed) % self.size
            if self.bit_array[result] == 0:
            	return "Nope"
        return "Probably"
1
2
3
4
5
6
7
bf = BloomFilter(500000, 7)
bf.add("scott")
bf.lookup("scott")
'Probably'

bf.lookup("zhang")
'Nope'

LRU Cache 缓存

Least Rencent Used,

  • 两个要素：大小、替换策略
  • 使用 Hash Table + Double LinkedList 实现
  • O(1) 查询，O(1) 更新、更新

工作示例

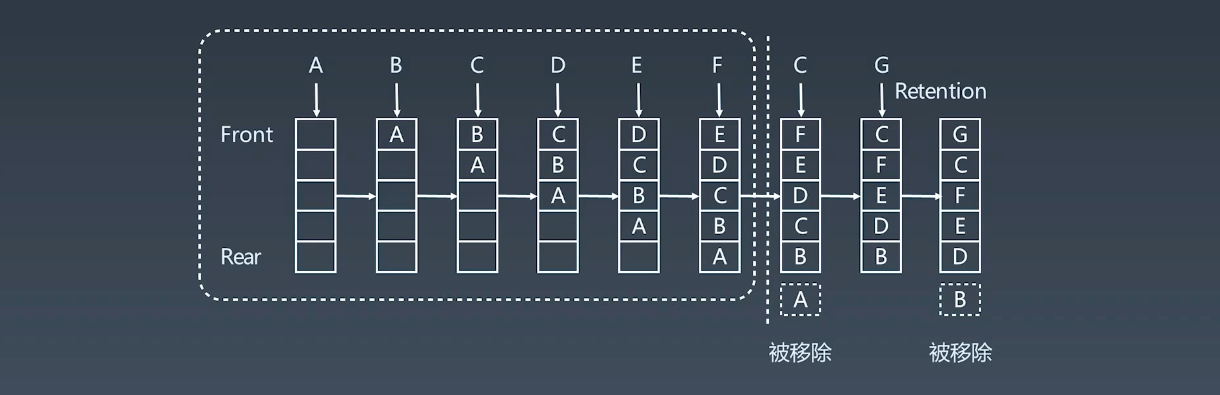
image.png

排序算法

To be continued.