Scikit-Learn 与监督学习

给机器学习的能力，让它可以根据数据自己做决定的一种技术。

机器学习

监督学习与非监督学习

什么是机器学习？它是给机器学习的能力，让它可以根据数据自己做决定的一种技术。

如，电子邮件是否是垃圾邮件，根据数据自动分类。

如果您使用的数据，是labled的，这就叫监督学习，如果是不unlabeled，则是非监督学习。

非监督学习的例子，如企业根据用户的数据，对用户进行分类(clustering).

clustering，非监督学习的一个分支。

Reinforcement learning

这是一种对系统进行奖赏与惩罚的训练技术，让机器可以根据环境的变化作出反应,典型的应用如阿法狗。

我们将首先focus在监督学习这部分。

我们将根据数据来训练，这些数据叫做 prodictor varibles 或者 features,indenpendent varibles，训练的目的是要做出预测，要预测的值叫做 target varibles,denpendent varibles或response varible, 如果预测的值是一组分类信息，如花的品种，人的性格，这种预测叫做classfication,如果是一些连续的值，如股票的价格，那就叫做regression.

现在我们先学习 classfication.

对于监督学习，首先需要数据，那么数据从哪里来？

• 历史的数据，已经做好了分类
• 通过自己的试验获取，如A/B Test

机器学习的工具有很多，我们主要是用 scikit-learn或者说sklearn.

其他的工具包括:

• TensorFlow
• keras

探索数据

示例数据

主要是用花瓣的数据，其中包括:

• petal lengh, 花瓣长度
• petal width，花瓣宽度
• sepal length，萼片 èpiàn 长度
• sepal width，萼片 èpiàn 宽度

萼片，即花瓣下面，包住花的那部分。

关于花，有不同的品种，在英文中叫做species，我们的数据中有三种，Iris Setosa（山鸢尾）、Iris Versicolour（杂色鸢尾），以及Iris Virginica（维吉尼亚鸢尾）。

数据怎么导入呢？

from sklearn import datasets
iris = datases.load_iris()

这是bunch类型的数据，跟python内置的dict数据差不多。

对于数据，记住,sample in rows, features are columns.

实例数据

美国众议员议员数据,US House of Representatives Congressmen.

我们去预测它们的政党隶属关系(party affiliation),即：

• 'Democrat',民主党
• 'Republican'，共和党

根据什么来预测呢？根据它们对特定问题的投票。

['party', 'infants', 'water', 'budget',
'physician', 'salvador','religious',
'satellite', 'aid', 'missile', 'immigration',
'synfuels','education', 'superfund',
'crime', 'duty_free_exports', 'eaa_rsa']

上面是数据集的列名，即一些议题的投票情况。

我们使用countplot图来探索这些数据，

plt.figure()
sns.countplot(x='education', hue='party', data=df, palette='RdBu')
plt.xticks([0,1], ['No', 'Yes'])
plt.show()

Classification

我们手头有labled的数据，但我们还需要对那些没有标记的数据进行标记，我们需要对标记过数据学习，然后建立一个标记器。

标记过的数据叫做traning data.

标记数据-KNN算法

我们用knn算法来实现这个步骤，knn是根据数据的邻居来预测的一种算法，比如放眼望全世界，如果您的位置在中国，那么我可以预测您有很大的几率是中国人，因为您和很多的中国人在一起，对于knn算法，我们首先需要根据knn算法建立模型并训练，训练模型我们叫fiting modal，在sklearn中，我们使用fit()方法，而predit()用来预测。

如:knn.fit(iris['data],iris['target'])

使用knn fit方法的条件:

1. np或者pd类型的数据
2. features是连续型的数据，不是分类数据
3. 没有缺失值

fit后，knn会返回fit后的分类器（classifier）本身，然后就可以拿来使用了。

示例：

# Import KNeighborsClassifier from sklearn.neighbors
from sklearn.neighbors import KNeighborsClassifier

# Create arrays for the features and the response variable
y = df['party'].values
X = df.drop('party', axis=1).values

# Create a k-NN classifier with 6 neighbors
knn = KNeighborsClassifier(n_neighbors=6)

# Fit the classifier to the data
knn.fit(X,y)

neighbors设置为6，这是这个示例默认的值，您可以设置成其他的值，在这个示例中，6是最合适的。

测试模型性能-Accuracy

accuracy是测试一个模型的指标，计算方法是模型的正确预测数/测试数据总数，那么我们用什么数据来算accuracy呢？

我们肯定需要用从来没有给模型用过的数据来计算，也不能用那些训练过模型的数据。

所以，一般的做法是，将数据分成两组：

1. traning set,用来训练模型
2. test set，用来预测，测试模型性能

我们用train_test_split 方法来实现，这个方法的参数中，

• x，y就不多介绍

• test_size为您要分隔的比例，一般来说traing占0.7，test占0.3

• stratify设置为y（y包含lable），这个参数可以让您的lable（分类数据）比较均匀的分布在分隔后的数据中，不至于过于集中

  训练完成之后，可以预测，然后就可以使用knn.score(x_test,y_testx)查看模型的分数。

另外对于n_neighbors，设置的值越大，则数据集之间的分界线（decision boundary）越不敏感，曲线变得更平滑，更少的波动，但太大会导致overfitting,而太小会导致underfiting。

Regression

regression问题是连续型的值的预测，如gdp, 房价。

我们对波士顿房价的数据进行预测，x值为一个街区中的房子房间的平均数量，可以观察到，房间数越多，价格越高。

regression的预测使用的是 linear_model模块。

线性回归基础

线性回归的基础就是y=a*x+b类似的一次函数,y是我们需要预测的值，x是我们的features，我们做的就是去寻找最合适的a与b，确定最合适的那个函数。

这么一个函数，我们叫做loss或者cost函数，我们为这个函数找到最合适的a与b值，让它确定的这个线，跟所有图中的点的的 垂直 距离最近，这里所说的距离就叫做 residual。

Residual

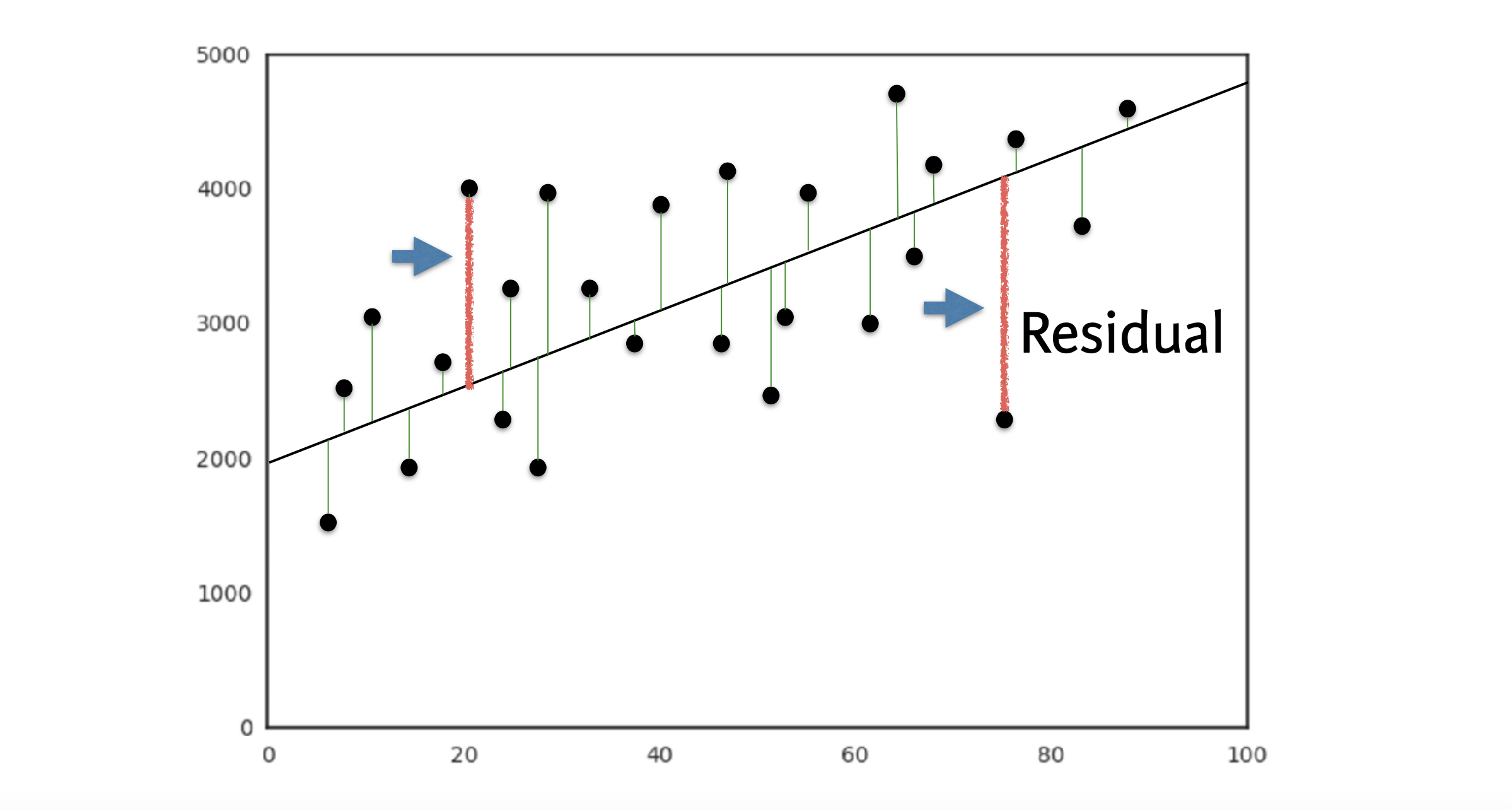
我们可以尝试减少所有 risidual 相加的和，但是正负会抵消，因为点距离线的距离有正负，那么我们减少这个距离的平方的和会比较好，即将所有的点与线段的距离平方后，再相加。

使用这个函数，就叫做最小二乘法（ordinary least squares）或者说OLS.

当我们训练的模型只有一个feature的时候，我们会使用 y=a*x+b,当feature增加到两个，则使用y=a1*x1+a2*x2+b,以此类推。

所以如果有两个feature的情况，我们的任务就是确定函数中三个数的值，a1,a2,b.

实例讲解

我们现在根据人的生育率来预测寿命，那么我们的x值就是生育率，我们会把它作为参数传给回归器，我们的生育率是有一个范围的，不可能为负数，也不可能是好几百，所以我们从收集到的真实数据中找到最小的和最大的作为生育率的范围。

# 导入相关的包
from sklearn.linear_model import LinearRegression

# 创建回归器
reg = LinearRegression()

# 确定生育率的范围，并reshape为回归器需要的shape（这里的数据是给预测器预测用的）
prediction_space = np.linspace(min(X_fertility), max(X_fertility)).reshape(-1,1)

# 把收集到的数据x与y传给回归器，让它学会怎么回归
reg.fit(X_fertility,y)

# 学会回归之后，把我们确定好的生育率范围数据传给预测器
y_pred = reg.predict(prediction_space)

# 打印 R^2 ，评分
print(reg.score(X_fertility, y))

# 绘图
plt.plot(prediction_space, y_pred, color='black', linewidth=3)
plt.show()

分割数据

我们提到过分割数据的概念，主要是使用train_test_split包方法。 分隔好数据后我们即可进行预测，预测后的数据使用回归器的score方法查看预测效果，另外这里还介绍一个对预测效果的打分工具，即mean_squared_error.

您可以通过 from sklearn.metrics import mean_squared_error 引入并使用它。

它又叫做 Root Mean Squared Error (RMSE).

它使用的参数是预测的数据与真实的数据：

# y_test已c好

y_pred = reg.predict(X_test)
rmse = np.sqrt(mean_squared_error(y_test,y_pred))

Cross-validation

RMSE的分数和您分割数据的方式是有关系的，我们需要一种科学的分割方式。 在test的数据中，可能会存在一种数据层面的 peculiarities 导致它不能代表模型对新数据的预测能力。 解决这个问题的技术就叫做 cross-validation,它将所有数据分组，并分别作为测试与训练组，这样便可以最大化训练的数据，同时也将所有的对所有的数据进行了预测。

先简单介绍下 cross-validation 的步骤：

1. 将数据分隔成5（或者别的）组，这里可以说组 group,也有人说fold
2. 将第一组作为test组，剩下的4组作为training组，training完成后，预测test组的数据，计算出结果作为标准（Metric1）
3. 将第二组作为test，重复直到最后一组(metric1,2,3,4,5)
4. 对5组metric进行统计分析，如mean，median，置信区间等等

分割成5组，即5folds = 5-fold CV, 10 folds = 10 folds CV,组数越多，所需要的计算量就大。

Regularized regression

回忆一下，我们对于线性回归的定义，我们找到与所有点的垂直距离最短的线,即确定这个一次函数的系数（coefficient），但如果我们让这些系数或者说参数很大，我们就会过度拟合（overfitting），所以我们需要控制这个系数（coefficient），如果coefficient变得很大，它就是不听话，那我们就对函数做出惩罚，我们知道regulation是合规的意思，这里的也就是说对regression的参数作出规范。

接下来我们会介绍一些常见的regulation。

Ridge regression 岭回归

ridge regression就是一个加强版的OLS loss function，它多了一个阿尔法参数，当阿尔法为0的时候，ridge regression变成了普通的ols函数，当阿尔法变得很大，对overfitting的惩罚也变得更大，更敏感，这会让模型变得过于简单(underfitting).

对于ridge regression的使用，它多了个alpha参数。另外对于不同参数，我们需要将它 归一化，所以在初始化ridge实例的时候，需要指定 normalize=true.

Lasso regression 套索回归

Lasson回归的特点是，它可以自己选择feature，这样就会把那些不重要features的系数降为或者说（shrink）为0.

当我们训练好模型后，我们可以通过 .coef_ 来查看模型中各个features的权重，或者说偏好。

下面是关于 coef_ 的解释。：

The coef_ contain the coefficients for the prediction of each of the targets. It is also the same as if you trained a model to predict each of the targets separately.

我们可以将columns与conef_绘图，这就可以看到哪些featues对模型的影响是最大的，这在许多的bussniss与科学实验中都有很多应用。

附：关于Lasso的Python实践

# Import Lasso
from sklearn.linear_model import Lasso

# Instantiate a lasso regressor: lasso
lasso = Lasso(alpha=0.4,normalize=True)

# Fit the regressor to the data
lasso.fit(X,y)

# Compute and print the coefficients
lasso_coef = lasso.coef_
print(lasso_coef)

# Plot the coefficients
plt.plot(range(len(df_columns)), lasso_coef)
plt.xticks(range(len(df_columns)), df_columns.values, rotation=60)
plt.margins(0.02)
plt.show()

Lasso非常适合选择features，但是在构建回归模型时，Ridge回归应该是您的首选。

关于阿尔法参数对ridge的影响，可以多研究研究这个章节。

调整模型

训练好模型之后，并不能完美的预测数据，就如打磨任何一件产品，粗加工后还需要细腻的打磨。这一节将会引入一些其他的metric来衡量您建立的模型，同时也会介绍优化模型的技术，即hyperparameter tuning.

在分类的问题中，accuracy是我们评价模型的标尺，但accuracy不总是唯一衡量模型的标准。

比如在垃圾邮件的检测问题中，如果我们把所有的邮件都作为正常邮件，因为我们只有1%的垃圾邮件。我们的模型准确度高达99%！听起来还不错，但这完全是个糟糕的模型

先记住，这种正常的数据远远多于异常数据的情况，叫做 class imbalance.

评价模型的标尺

给定一个两个结果的分类器，如垃圾邮件问题：

	预测到的垃圾邮件	预测到的真实邮件
实际为垃圾邮件	True Positive	False Negative
实际为真实邮件	False Positive	True Negative

上面的这个表，叫做confusion matrix

• 左上和右下的为预测正确的情况
• 通常，感兴趣的组为positive，想要预测垃圾邮件，那么垃圾邮件即为positive的

为什么需要confusion matrix?

1. 计算Accuracy,即：对角线（diagonal）格子数/格子总数, tp+tn/(tp+tn+fp+fn)
2. 计算其他的模型指标，如：
   3. Precision，又叫positive predictive,PPV: tp/(tp+fp),在垃圾邮件模型中为，实际垃圾邮件数量/预测垃圾邮件数量；这个指标值越高，意味着我们更少的真实邮件预测为垃圾邮件，提高precision则我们的预测更准确，它又叫做准确率，查准率
   4. Recall，tp/(tp+fn),预测正确的垃圾邮件占所有实际垃圾邮件之比，提高recall即意味着尽可能多的预测所有垃圾邮件，所以它也叫做查全率或叫召回率
   5. F1score,2*(precision*recall/precision+recall)，Precision与recall分别对应查准问题与查全问题，然而常常二者不能同时提高，所以对于实际复杂问题处理很有偏见，于是我们引入F1-score来近似帮助我们解决实际问题。

可以直接使用confusion matrix函数来计算，它接受两个数据，一个是y_test,另一个是y_pred，即预测出来的数据。

对于 resulting matrix, 也是一样的，在所有的sklearn的预测函数中，第一个参数总是test数据，第二个一般都是预测出来的数据,另外还有一个support参数，它就是test数据中对于不同结果的响应情况，总数就是test数据的长度。

Logistic regression

不要被这个名字迷惑，logistic regression其实是用来处理分类问题的。

它返回的是概率，当预测的数据概率大于0.5，我们标记为1，如果小于0.5，则标记为0.

它有点像线性回归，会在图像上把两组数据区分开来,这个边界就叫做线性决策边界（linear decision boundary）

在使用logistic regression的时候，我们可以定义这个概率（默认是0.5）.

• 如果定为0，那么所有进来的数据全部预测为1
• 如果定为1，所有进来的数据全部预测为0

ROC 曲线

根据我们之前定义的混淆矩阵，我们再来了解两个指标,方便我们引入ROC的概念：

	预测到的垃圾邮件	预测到的真实邮件
实际为垃圾邮件	True Positive	False Negative
实际为真实邮件	False Positive	True Negative

假设我们有如下的图：

ROC曲线

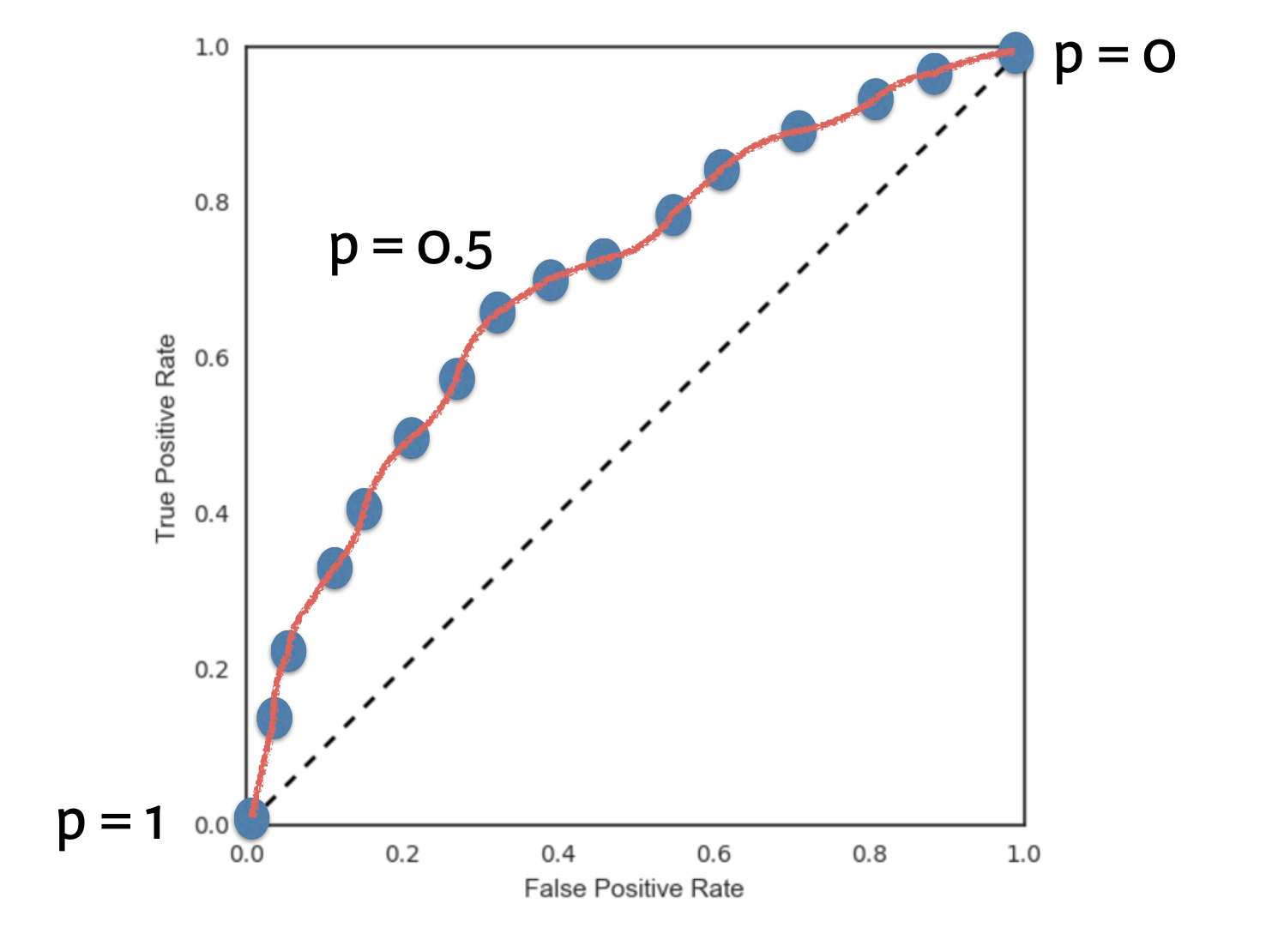
• FPR, fpr = fp/(fp+tn),FPR表示，在所有的垃圾邮件中，被预测成正常邮件的比例。它告诉我们，随机拿一个垃圾邮件，有多大概率会将其预测成正常邮件。显然我们会希望FPR越小越好。

• TPR，fpr=(tp/tp+fn), TPR表示，在所有的正常邮件中，被预测为正常邮件的比例，即随机拿一个正常邮件，有多大的概率会被预测称正常邮件，我们希望这个值越大越好。

x轴是FPR，y轴是TPR，那么点（0，0），（1，1）意味着什么呢？

• （0，0）即FPR=0，TPR=0，也就是FP=0，TP=0，意味着，所有的邮件，我都把它预测为垃圾邮件
• （1，1）意味着，所有邮件，我都预测为正常邮件
• (1,0)，即FPR=1，TPR=0，这是最糟糕的情况。所有的预测都预测错了
• 点(0,1)，FPR=0说明FP=0，也就是说没有一个真实邮件被看作垃圾邮件，TPR=1，即所有正常邮件都是标记成正常邮件，这是最好的情况

我们知道，在二分类（0，1）的模型中，一般我们最后的输出是一个概率值，表示结果是1的概率。那么我们最后怎么决定输入的x是属于0或1呢？我们需要一个阈值，超过这个阈值则归类为1，低于这个阈值就归类为0。所以，不同的阈值会导致分类的结果不同，也就是混淆矩阵不一样了，FPR和TPR也就不一样了。所以当阈值从0开始慢慢移动到1的过程，就会形成很多对(FPR, TPR)的值，将它们画在坐标系上，就是所谓的ROC曲线了。

引用自CSDN博主「Webbley」的原创文章。

建立Logistic modal

# Import the necessary modules
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import confusion_matrix,classification_report

# Create training and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.4, random_state=42)

# Create the classifier: logreg
logreg = LogisticRegression()

# Fit the classifier to the training data
logreg.fit(X_train,y_train)

# Predict the labels of the test set: y_pred
y_pred = logreg.predict(X_test)

# Compute and print the confusion matrix and classification report
print(confusion_matrix(y_test, y_pred))
print(classification_report(y_test, y_pred))

绘制ROC曲线

# 引入roc的包
from sklearn.metrics import roc_curve

y_pred_prob = logreg.predict_proba(X_test)[:,1]
fpr, tpr, thresholds = roc_curve(y_test, y_pred_prob)

plt.plot([0, 1], [0, 1], 'k--')
plt.plot(fpr, tpr, label='Logistic Regression')
plt.xlabel('False Positive Rate’)
plt.ylabel('True Positive Rate')
plt.title('Logistic Regression ROC Curve')
plt.show();

ROC曲线下面的面积

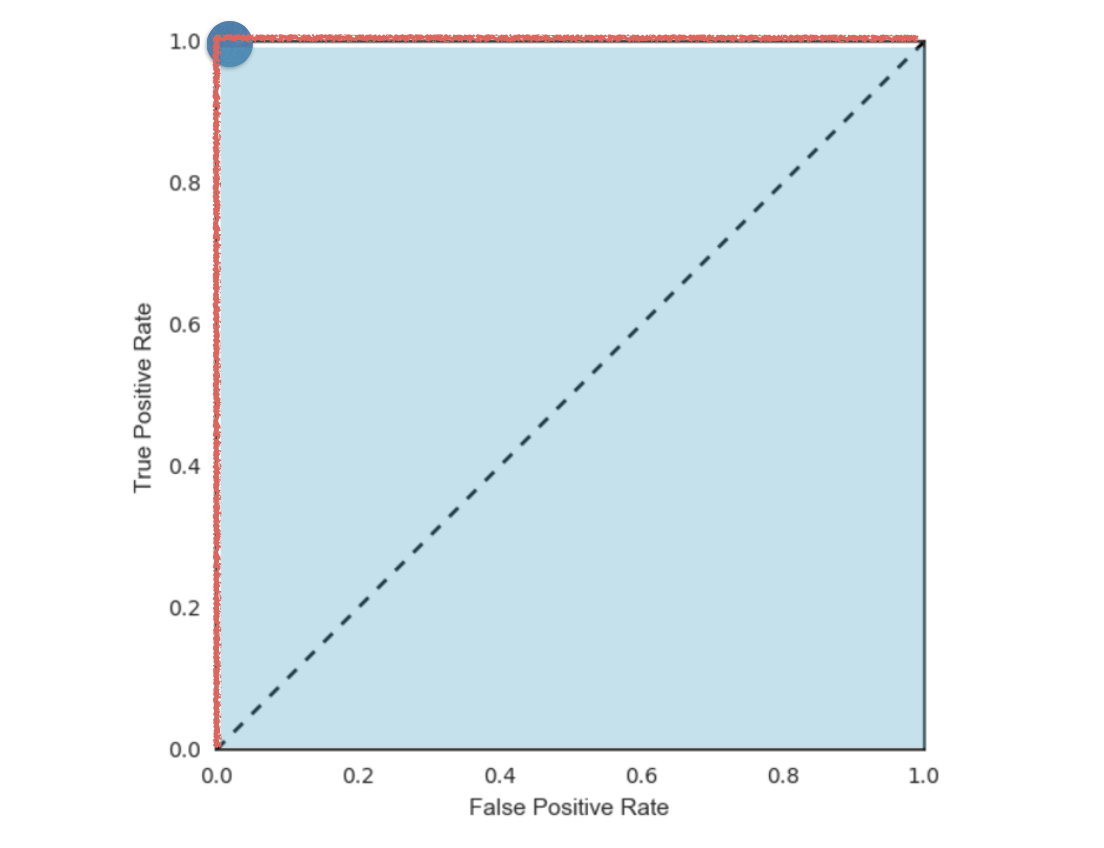
当我们的FPR与TRP位于（0，1）的时候，预测到的结果是最好的，观察这个ROC图像，即ROC曲线下面的面积最大的时候，所以我们可以得出:

ROC曲线下面的面积越大，模型越好！

这个面积就叫做AUC，同样也是一个使用广泛的分类问题评价标尺。

计算AUC

# Import necessary modules
from sklearn.metrics import roc_auc_score
from sklearn.model_selection import cross_val_score

# Compute predicted probabilities: y_pred_prob
y_pred_prob = logreg.predict_proba(X_test)[:,1]

# Compute and print AUC score
print("AUC: {}".format(roc_auc_score(y_test, y_pred_prob)))

# Compute cross-validated AUC scores: cv_auc
cv_auc = cross_val_score(logreg,X,y,cv=5,scoring='roc_auc')

# Print list of AUC scores
print("AUC scores computed using 5-fold cross-validation: {}".format(cv_auc))

Hyperparameter tuning

• 线性回归：选择参数
• ridge/lasso: 选择alpha
• KNN：选择neighbors

上面这些选择的参数，就叫做Hyperparameter tuning。

所以一个好的模型，就在于选择一个好的参数，这个参数如何决定呢？

我们可以定义一个grid表格，将参数填进去，一个一个的试验，直到找到最好的那个。

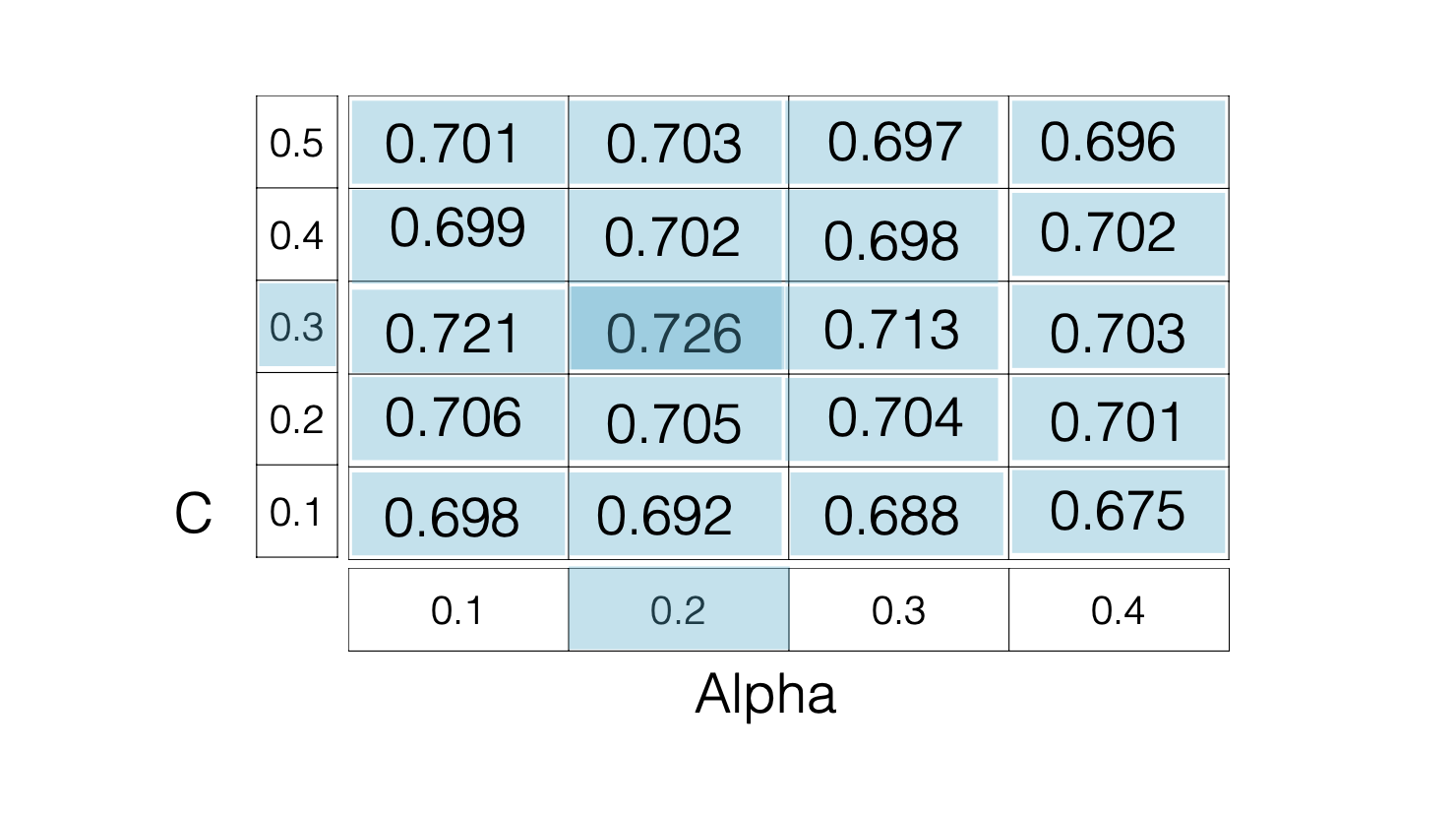
Grid search cross-validation

GridSearchCV

# Import necessary modules
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import GridSearchCV

# Setup the hyperparameter grid
c_space = np.logspace(-5, 8, 15)
param_grid = {'C': c_space}

# Instantiate a logistic regression classifier: logreg
logreg = LogisticRegression()

# Instantiate the GridSearchCV object: logreg_cv
logreg_cv = GridSearchCV(logreg, param_grid, cv=5)

# Fit it to the data
logreg_cv.fit(X,y)

# Print the tuned parameters and score
print("Tuned Logistic Regression Parameters: {}".format(logreg_cv.best_params_))
print("Best score is {}".format(logreg_cv.best_score_))

RandomizedSearchCV

上面的searchCV是按照一定的规则来测试参数，而randomizedSearchCV则是随机选择数据作为测试的参数，代码如下：

# Import necessary modules
from scipy.stats import randint
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import RandomizedSearchCV


# Setup the parameters and distributions to sample from: param_dist
param_dist = {"max_depth": [3, None],
              "max_features": randint(1, 9),
              "min_samples_leaf": randint(1, 9),
              "criterion": ["gini", "entropy"]}

# Instantiate a Decision Tree classifier: tree
tree = DecisionTreeClassifier()

# Instantiate the RandomizedSearchCV object: tree_cv
tree_cv = RandomizedSearchCV(tree, param_dist, cv=5)

# Fit it to the data
tree_cv.fit(X,y)

# Print the tuned parameters and score
print("Tuned Decision Tree Parameters: {}".format(tree_cv.best_params_))
print("Best score is {}".format(tree_cv.best_score_))

数据预处理与管道

现实世界的数据是复杂的，我们目前使用的都是标记过的数据，如果是没有标记过的数据，我们就需要将其打上标记，我们可以使用pandas的get_dummies()方法或者是sklearn的OneHotEncoder()，它会完成数据之间的转换，如下所示:

原始数据：

	origin
0	US
1	Europe
2	Asia

get_dummies()后：

origin_Asia	origin_Europe	origin_US
0	0	1
0	1	0
1	0	0

对于dummies后的数据，如果我们已经有了前两列（origin_Asia,origin_Rurope）的数据，就可以推测剩下的就是US的数据了，所以可以把US这里列删掉。

处理missing data

您收集到的数据，不会是完美的，肯定有些值是缺失的，它们可能为0，为nan，或者以其他形式记录的空值。

你可以使用np.dropna来把所有为空值的行删除，但这样很可能会让你的数据总量变少。

你也可以自动将所有的空值，以该列的平均值替代。

可以利用imputer对象来处理，如:

imp = impImputer(missing_values='NaN',strategy='mean',axix=0)

imp.fit(X)
imp.transform(X)

用imp fit X后，便可对数据进行transform，因此imputer对象也叫transformer.

管道

将你的操作打包成一个数组，就变成了一个pipline，你可以把你的操作（如处理missing value，大小写转换等等）都写进管道，一次性处理。

# Import necessary modules
from sklearn.preprocessing import Imputer
from sklearn.pipeline import Pipeline
from sklearn.svm import SVC

# Setup the pipeline steps: steps
steps = [('imputation', Imputer(missing_values='NaN', strategy='most_frequent', axis=0)),
        ('SVM', SVC())]

# Create the pipeline: pipeline
pipeline = Pipeline(steps)

# Create training and test sets
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.3,random_state=42)

# Fit the pipeline to the train set
pipeline.fit(X_train, y_train)

# Predict the labels of the test set
y_pred = pipeline.predict(X_test)

# Compute metrics
print(classification_report(y_test, y_pred))

Centering and scaling

模型的featuers的数据值，它的取值范围可能是非常大的，比如年龄的区间是0-100，而体重的区间则不一样。对模型来说，我们最好将这些数据进行缩放（scaling），全部放到同一个区间中，这样它们对于模型的重要程度才比较好估计。

缩放的范围可以是0-1，也可以是-1到1.

可以查看sklearn的文档，了解更多关于scaling的细节。