Scott's Blog

学则不固, 知则不惑

0%

优先队列与堆

发表于 更新于 分类于 阅读次数： Valine：

优先队列 Priority Queue (PQ) 是一个抽象的数据结构，堆（heap）是一个具体的数据结构，可以说是优先队列的一个实现。

优先队列

优先队列至少需要有以下这些操作：

  • is_empty, 队列是否为空
  • add_element, 增加元素
  • pop_element, 弹出元素

Python 有一个优先队列的实现，即堆（heapq），其中最小的元素拥有最高的优先级。它的每个父节点的值都只会小于或等于所有孩子节点（的值）; 最小的元素总是在根结点：heap[0]

Python heapq 模块和一般的堆数据结构，在设计时不允许查找除最小元素之外的任何元素。对于按大小检索任何元素，更好的选择是二叉搜索树。

堆使用了完全二叉树来实现优先队列，这意味着树的深度等于2为底，元素个数的对数。堆中每个父节点的值都小于或等于其任何子节点，这一点与二叉搜索树不一样（子节点中左节点小于右节点）

优先队列在编程中应用广泛，特别是那些需要在一些元素中查找极端值的情况，比如：

  • 根据点击量，查找博客中最受欢迎的5篇文章
  • 找出从 a 点到 b 点最快的路径
  • 你有发送邮件的一些任务，其中一些邮件需要每5分钟发一次，另外的一些需要每4分钟发一次

在 heapq 模块中作为列表的堆

堆是一个完全二叉树，我们可以使用列表来表示（下图表示的为最大堆）：

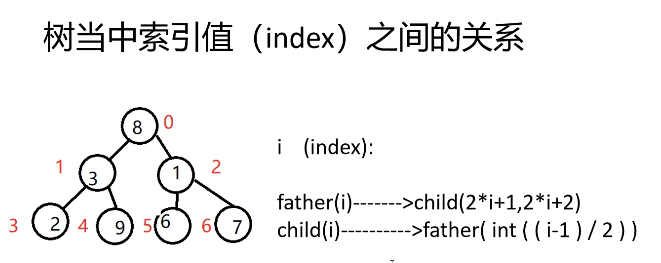
数组表示堆
  • 用 i 来表示索引值（也有用 k）
  • 作为父节点，它的第一个子节点的数组下标为 2*i + 1.
  • 作为父节点，它的第二个子节点数组下标为 2*i + 2.
  • 作为子节点，它的父节点为 (i - 1) // 2.

Python 中最小堆的一个特性，即子节点都要大于父节点，可以表示为：

1
h[i] <= h[2*i + 1] and h[i] <= h[2*i + 2]

操作堆

Python 中堆的实现是依赖于 list 的，它没有使用自定义的类。

可以从一个空堆开始初始化数据，但是如果你已经有一个list需要将其中的元素放到堆中，则可通过 heaptify() 来把一个 list 转成堆。

1
2
3
4
5
import heapq
a = [3, 5, 1, 2, 6, 8, 7]
# heapify() 修改列表，但不对它进行排序。
heapq.heapify(a)
a[2]

可以通过堆来实现优先级任务：

1
2
3
4
5
6
h = []
heappush(h, (5, 'write code'))
heappush(h, (7, 'release product'))
heappush(h, (1, 'write spec'))
heappush(h, (3, 'create tests'))
heappop(h)

再来看一个前面提到的发送 email 的例子：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
import datetime
import heapq

def email(frequency, details):
    current = datetime.datetime.now()
    # 产生一个无限循环的生成器
    while True:
        current += frequency
        yield current.strftime("%Y/%m/%d %H:%M") , details

fast_email = email(datetime.timedelta(minutes=15), "fast email")
slow_email = email(datetime.timedelta(minutes=40), "slow email")

# 将两个生成器在 heapq 中 merge
unified = heapq.merge(fast_email, slow_email)

我们调用结合后的生成器 10 次看看结果：

1
2
for i in range(10):
    print(next(unified))

输出如下：

1
2
3
4
5
6
7
8
9
10
('2022/02/08 17:40', 'fast email')
('2022/02/08 17:55', 'fast email')
('2022/02/08 18:05', 'slow email')
('2022/02/08 18:10', 'fast email')
('2022/02/08 18:25', 'fast email')
('2022/02/08 18:40', 'fast email')
('2022/02/08 18:45', 'slow email')
('2022/02/08 18:55', 'fast email')
('2022/02/08 19:10', 'fast email')
('2022/02/08 19:25', 'fast email')

可以看到 fast email 是间隔 15 分钟每次发送，而 slow email 则是40 分钟一次，它们完美的交错成一个任务列表。

merge 并不会一次性将所有输入全部读取，所以即使我们传入的无限重复的生成器，它也非常快且不占用很多内存。

使用堆的其他场景

堆还擅长解决统计最大或者最小的问题，比如下面这个统计得奖次数得例子：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import heapq
results="""\
Christania Williams      11.80
Marie-Josee Ta Lou       10.86
Elaine Thompson          10.71
Tori Bowie               10.83
Shelly-Ann Fraser-Pryce  10.86
English Gardner          10.94
Michelle-Lee Ahye        10.92
Dafne Schippers          10.90
"""
top_3 = heapq.nsmallest(
    3,                                  # 指示返回多少个元素
    results.splitlines(),               # 分割成数组，要比较的元素或数据集
    key=lambda x: float(x.split()[-1])  # 确定如何比较元素的可调用函数
)
print("\n".join(top_3))

输出如下：

1
2
3
Elaine Thompson          10.71
Tori Bowie               10.83
Marie-Josee Ta Lou       10.86