今天开始准备对机器学习相关概念做个总结,part1会包括以下概念:Cross Validation、Confusion Matrix、Sensitivity 与 Specificity、Bias 与 Variance、ROC 与 AUC、Odds Ratios 与 Log(Odds Ratios)。
Cross Validation
假设你需要根据肩膀痛、血液状况、动脉阻塞、体重与否来预测患者有没有心脏病,输出的结果为是与否。 当你对数据进行训练的时候,你需要指定使用的机器学习模型,常用的比如:
- LR
- KNN
- SVM
但你怎么知道选择哪一种模型呢?Cross Validation 可以让我们大概知道哪些模型会fit比较好,哪些模型在实际应用的时候表现会更好。
当训练模型的时候,需要将数据切割成训练组与测试组。如果你把所有的数据都拿去训练,那你就没有了测试数据,因为你的模型必须用它没有见过的数据来做测试。
通常我们使用数据中的前面百分之75的数据作为训练数据
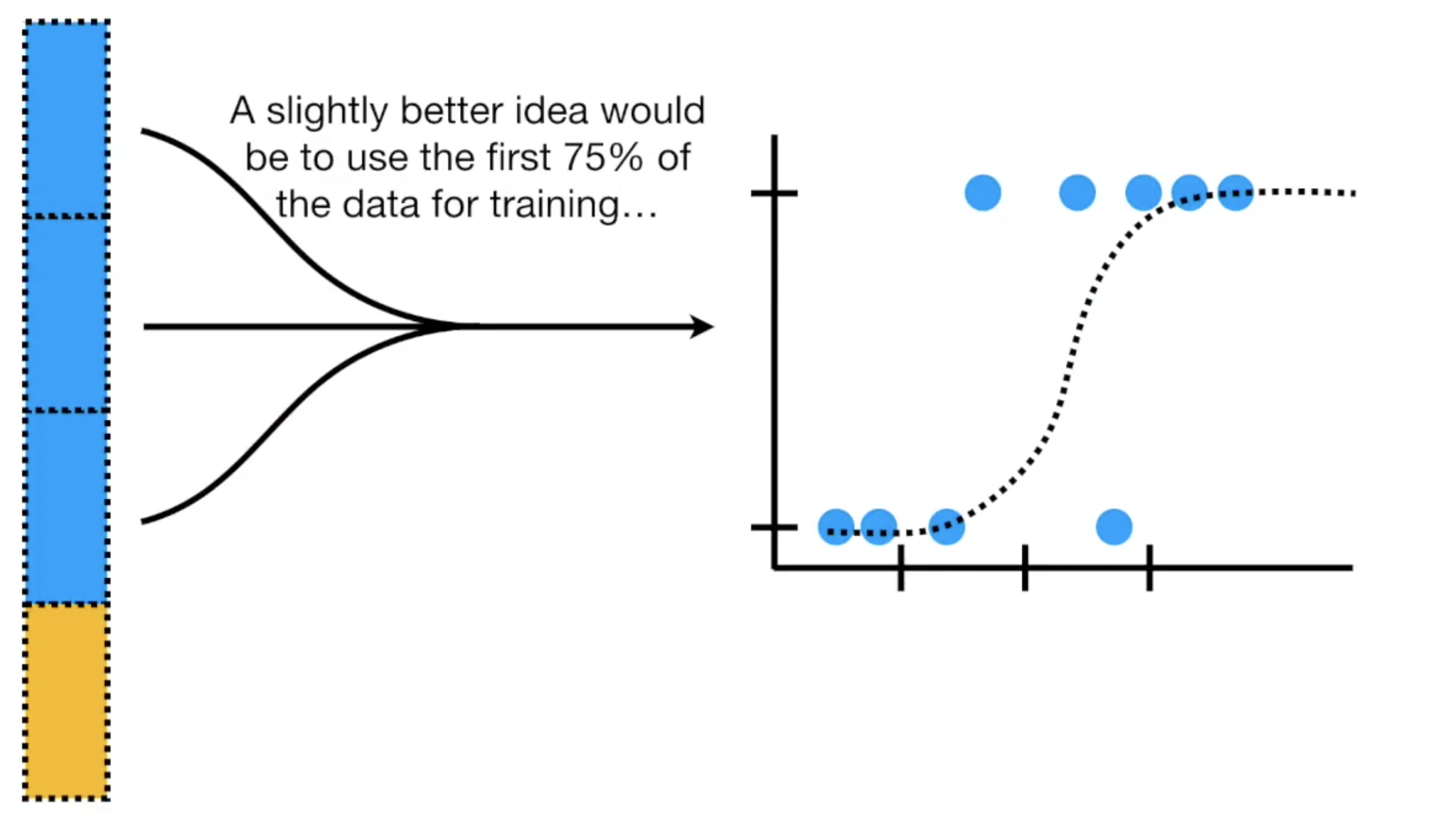
后面的部分作为测试数据
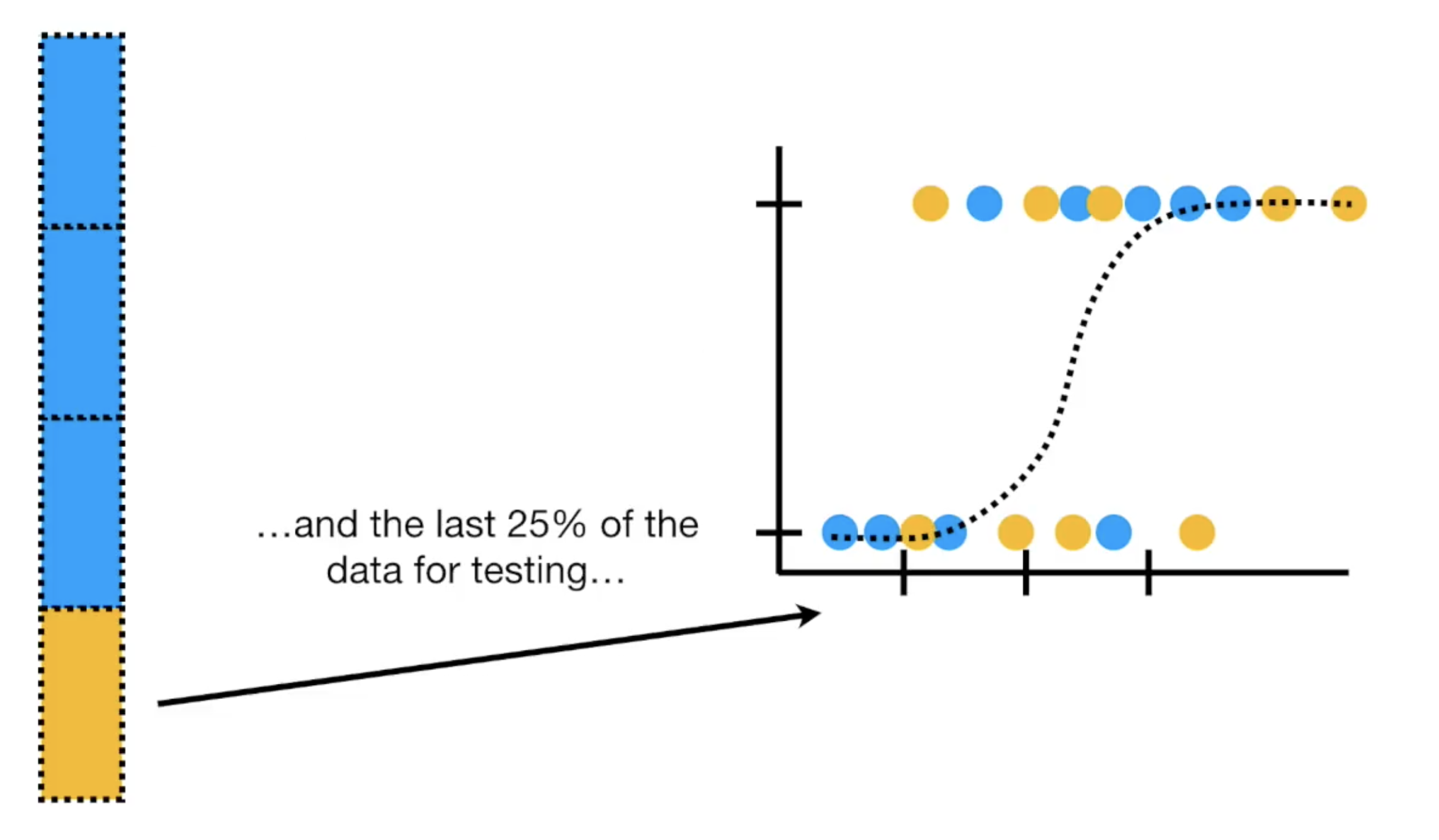
但是你怎么知道按照75:25的划分是最好的呢?如果我们使用前面百分之25的数据测试呢?或者是取中间的25%测试,其余的作为训练数据?
担心选择哪一段数据作为训练和测试数据,我们用Cross Validation,它会逐一将所有的数据都测试一遍,然后汇总结果。这样每一组数据都作为测试数据参与过模型训练,也参与过模型的检测。逐一测试后,再汇总所有结果,我们就可以选择最适合数据的模型。
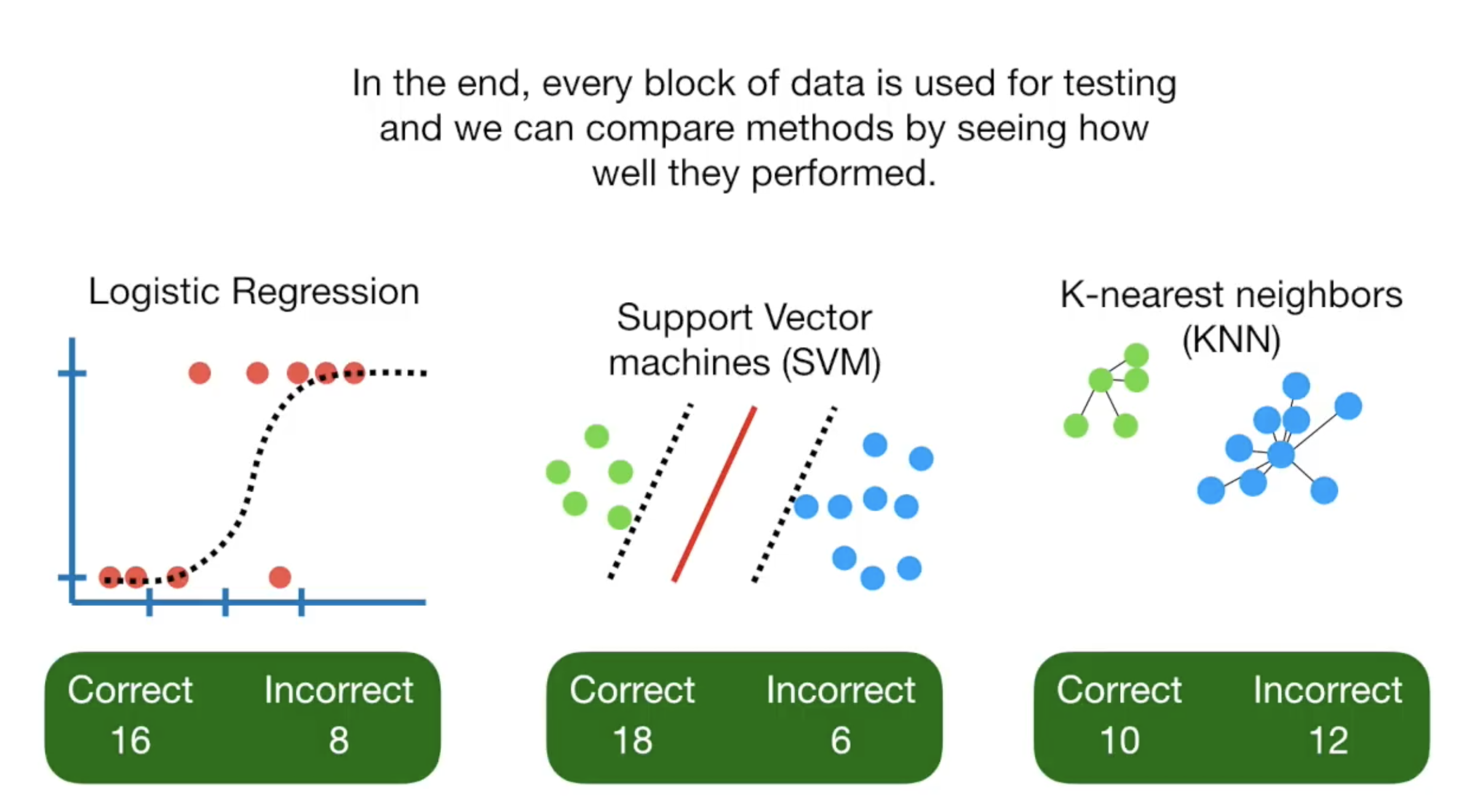
在这,如果你把数据分成4份,就叫4-Fold Cross Validation, 5份就叫5fold,以此类推。
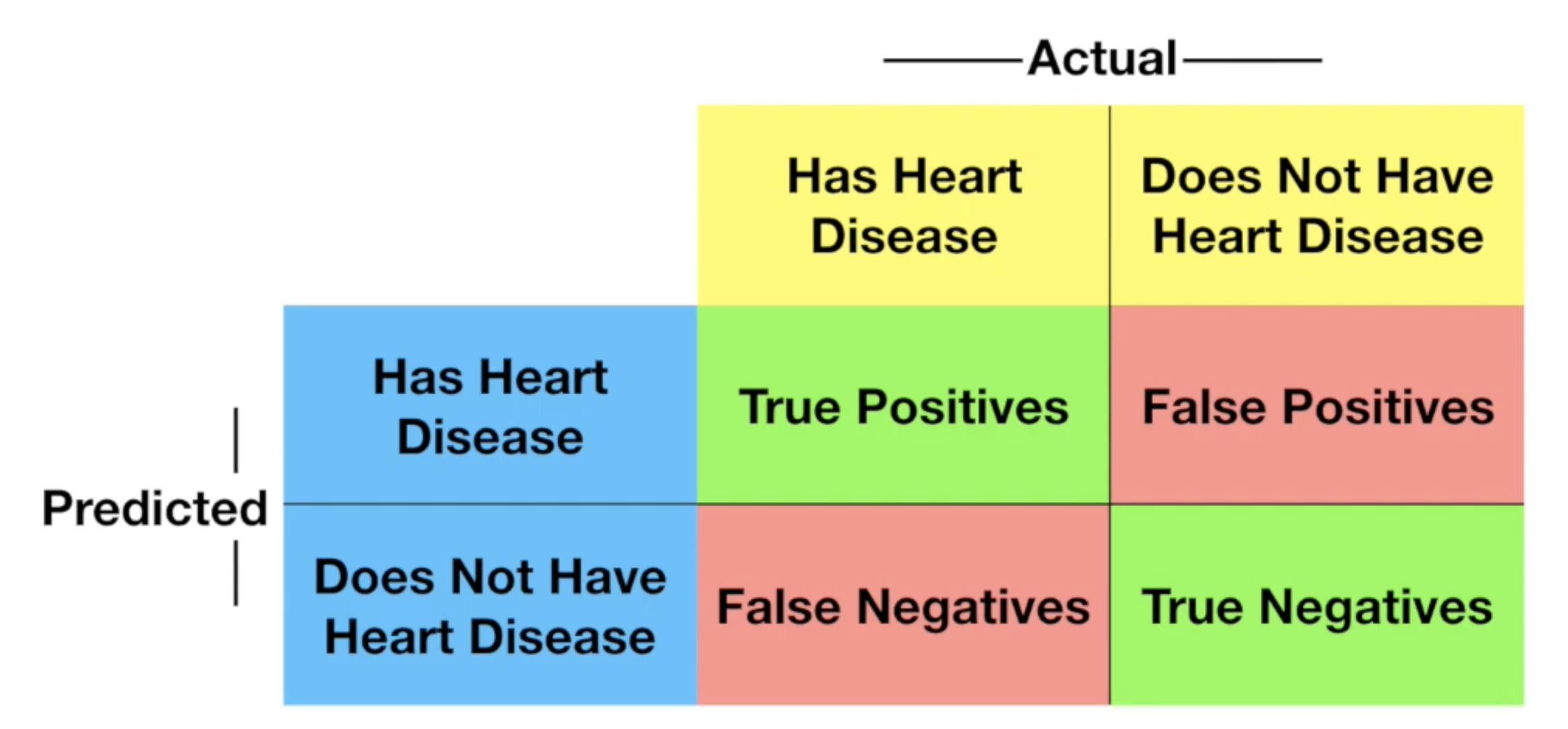
Confusion Matrix
Confusion Matrix这个概念告诉我们,机器学习的算法预测的结果中,正确了多少、错了多少以及正确的分布在哪里,错的又分布在哪里。

比如这个例子中,我们想要根据肩膀痛、血液状况、动脉阻塞、体重与否来预测患者有没有心脏病,输出的结果为是与否。
我们可以使用逻辑回归、knn、随机森林等模型来预测,或者你也可以使用任何其他的模型,但是我们如何来衡量这个模型的好坏呢?
首先将数据切分成训练组与测试组,在对上述模型进行训练之后,我们可以拿模型来对测试组的数据进行测试,然后将预测的结果与实际的结果进行对比,根据下面的表填入结果:
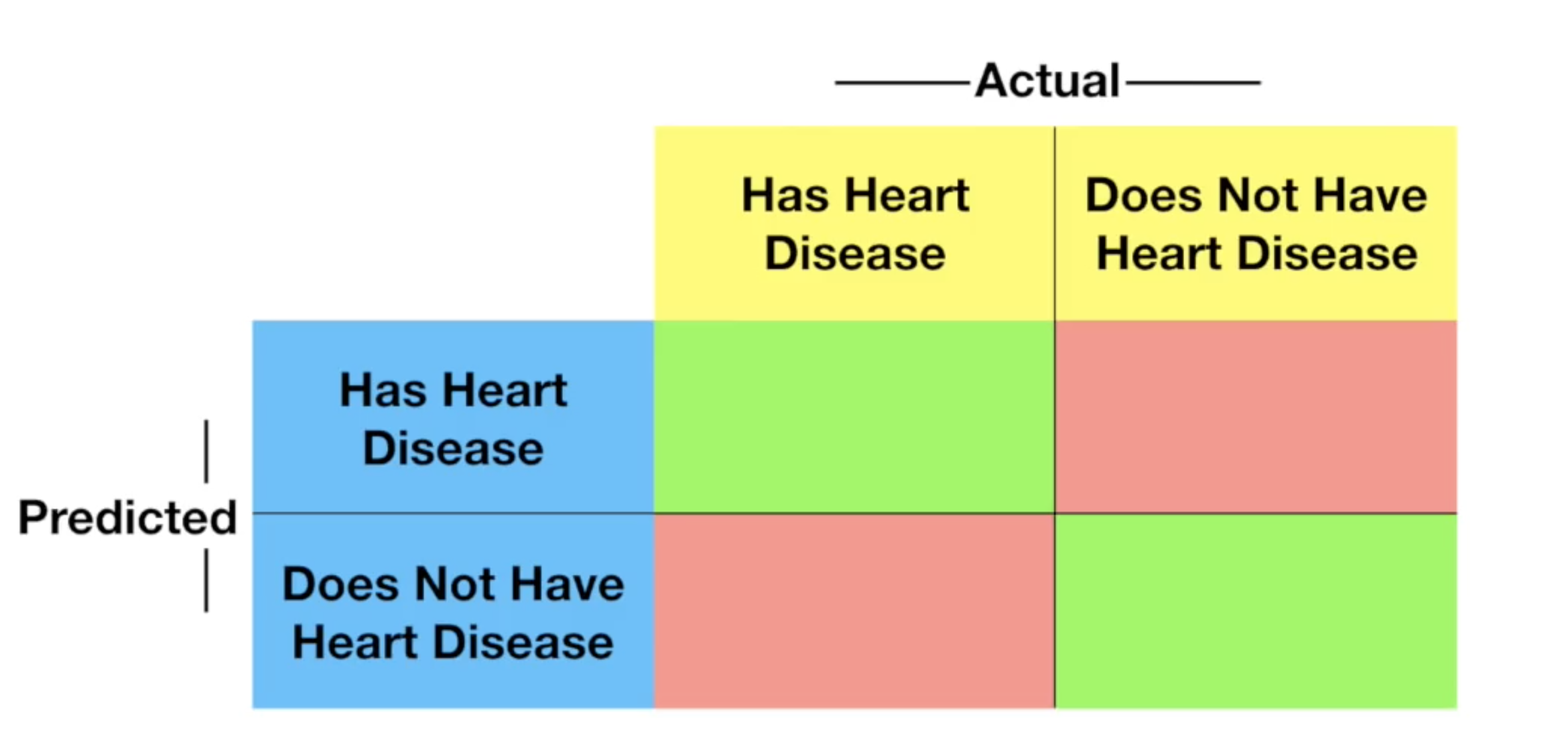
通过这个表,就可以知道你的模型预测的结果分布如何,对于每一个模型我们都可以绘制此表用来对比模型的性能。
Sensitivity 与 Specificity
在你理解了Confusion Matrix之后,我们再来讨论Sensitivity 与 Specificity.
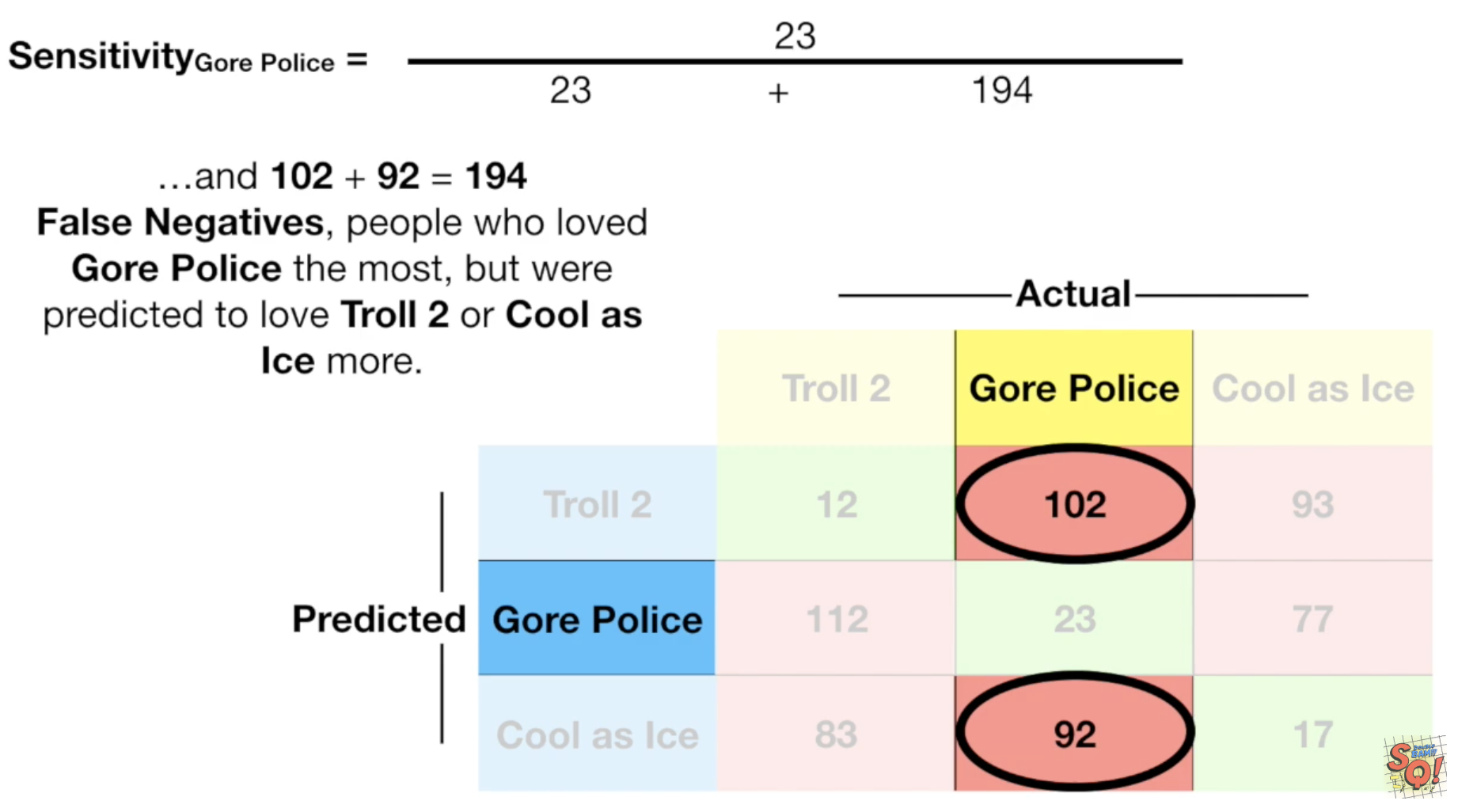
这里的Sensitivity,也可以理解为我们在sklearn课程中提及到的Recall,它等于 tp/(tp+fn),即所有有心脏病的人中,多少预测对了;
这是Sensitivity的计算: 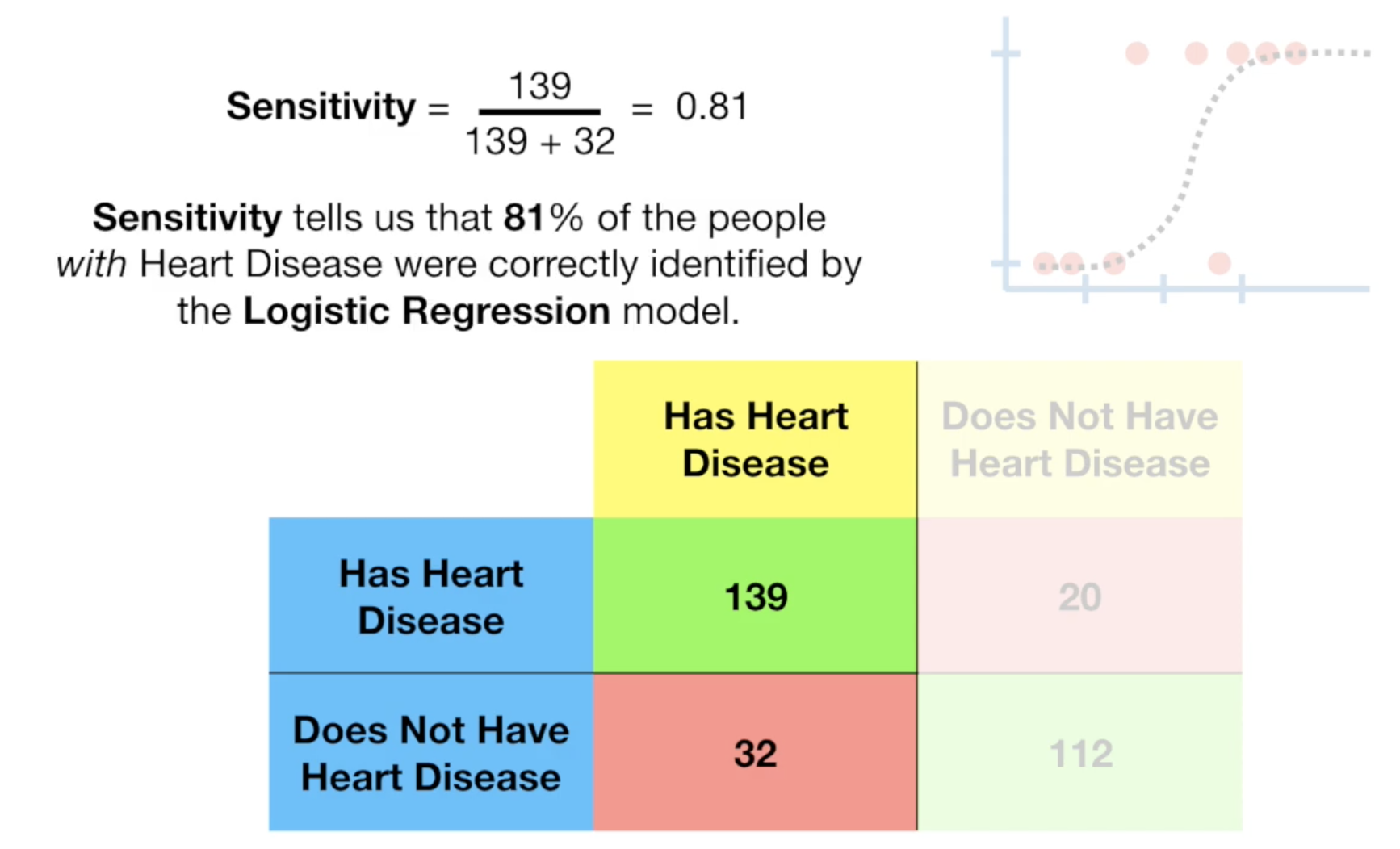
而Specificity,等于 tn/(tn+fp),即所有真实没有心脏病的人中,多少预测对了。 这是Specificity的计算: 
我们可以对不同的模型(如LR与随机森林)计算它们的Sensitivity 和 Specificity做比较。
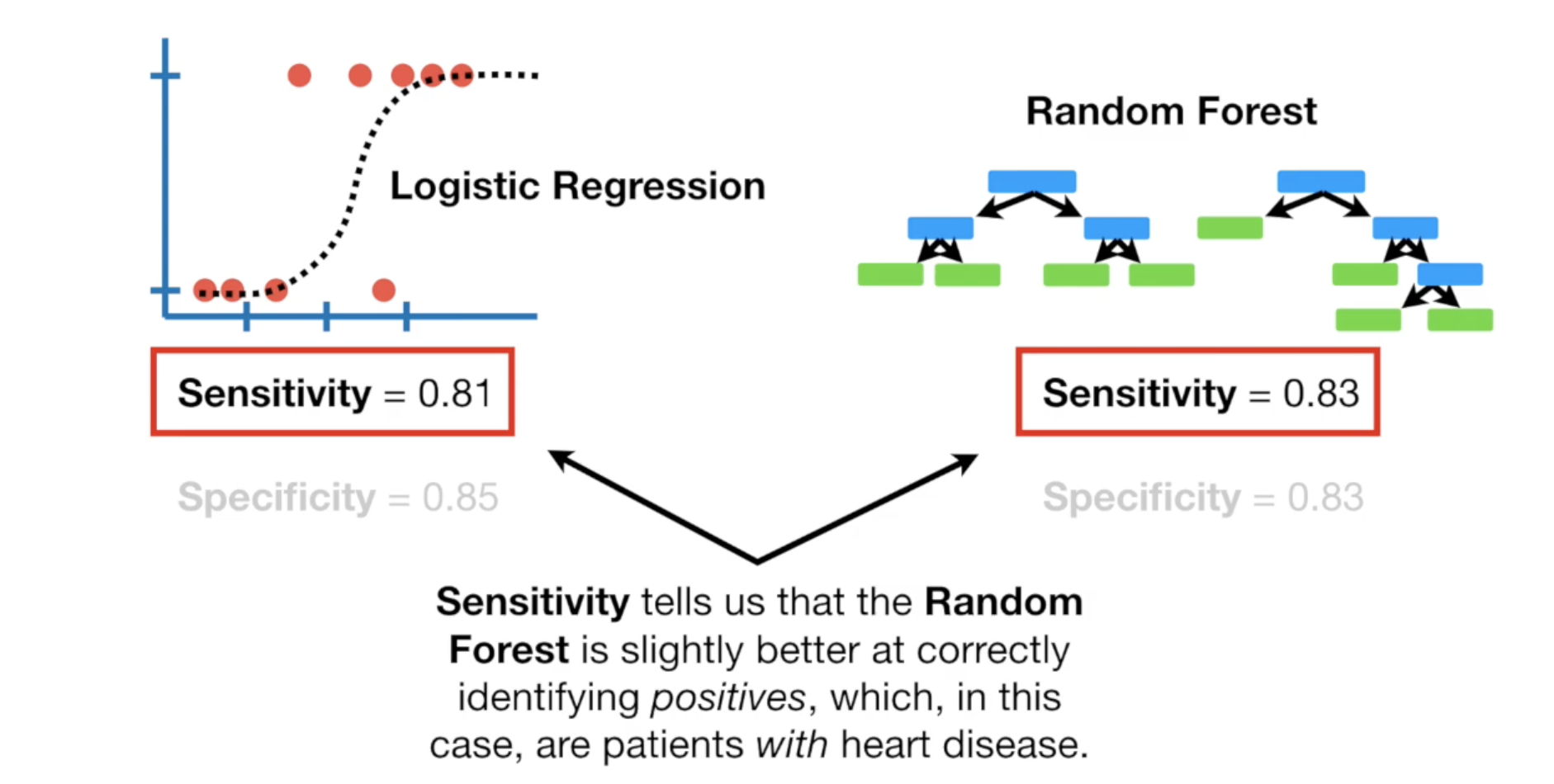
可以看到随机森林的sensitivity分数比较高,这意味着它对于区分positives的结果比较擅长,也就是预测哪些病人有心脏病。
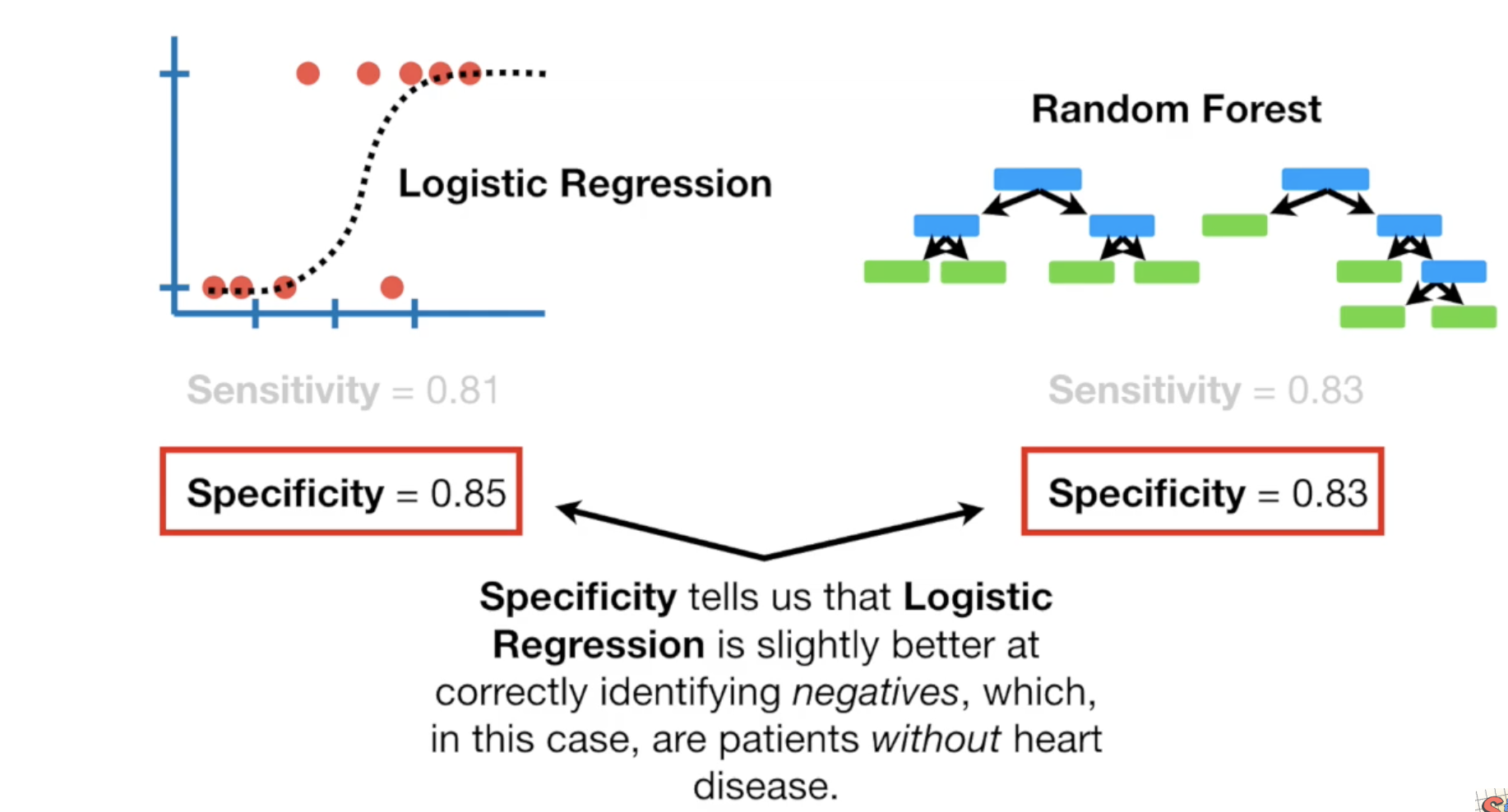
而LR则在预测哪些病人没有心脏病方面比较擅长。
如果对你来说,更重要的是找出那些人有心脏病,那么你应该使用随机森林,如果你更看重那些人没有心脏病,那么应该使用LR.
如果你的Confusion Matrix是三行三列,那么计算方式就不一样了,不过也没那么复杂,注意好对应关系就好了:

更多请参考油管视频.
Bias 与 Variance
你有一组老鼠的长度与体重数据,可以想象,老鼠的重量与长度是正比的,但它长到一定长度后,重量不会一直增长。我们使用LR训练一批老鼠数据,得到下面的图像:
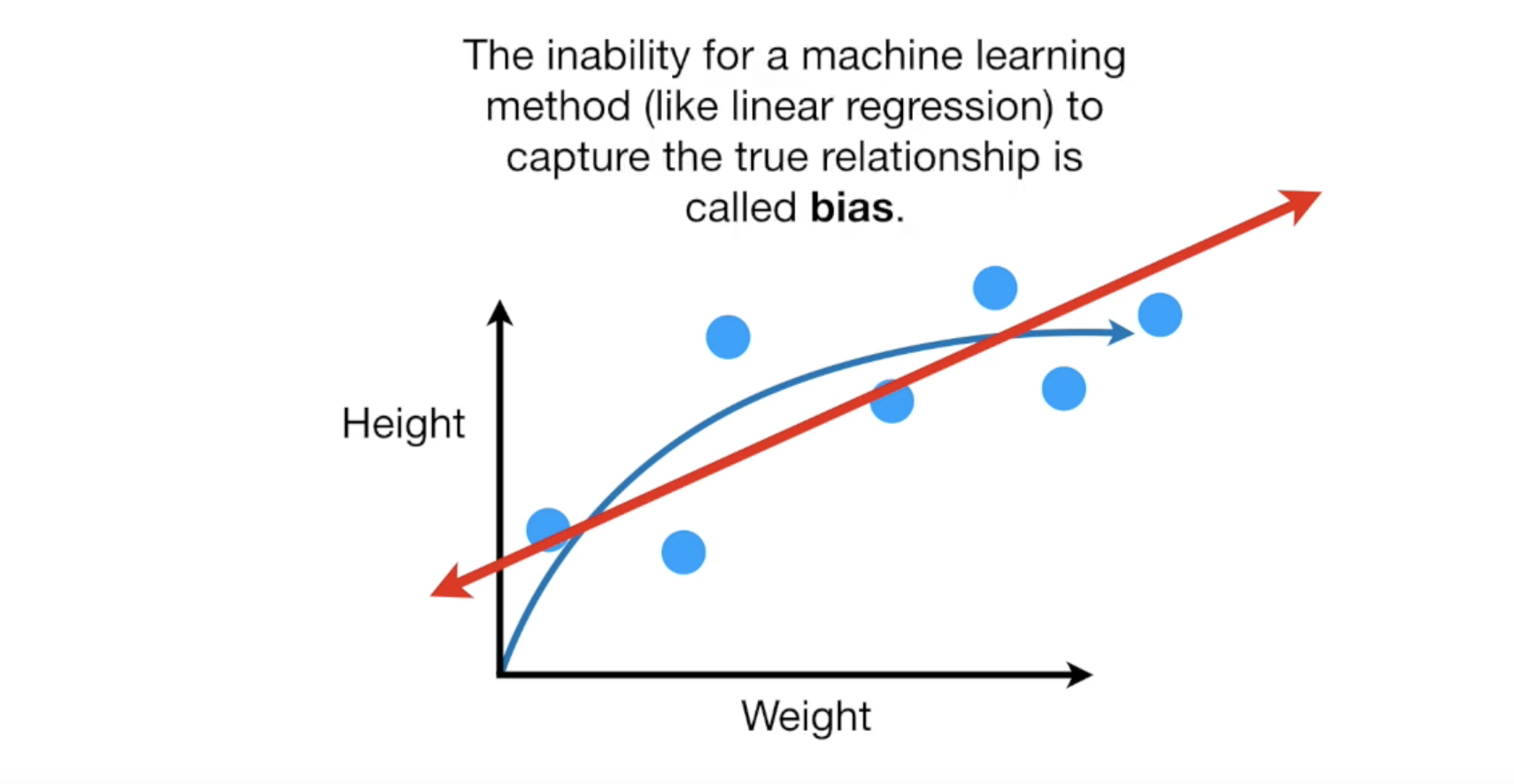
LR无法完全与训练数据重合,这就叫做bias,你的模型也可能完美的穿过这些测试数据,这样它的模型bias就为0.
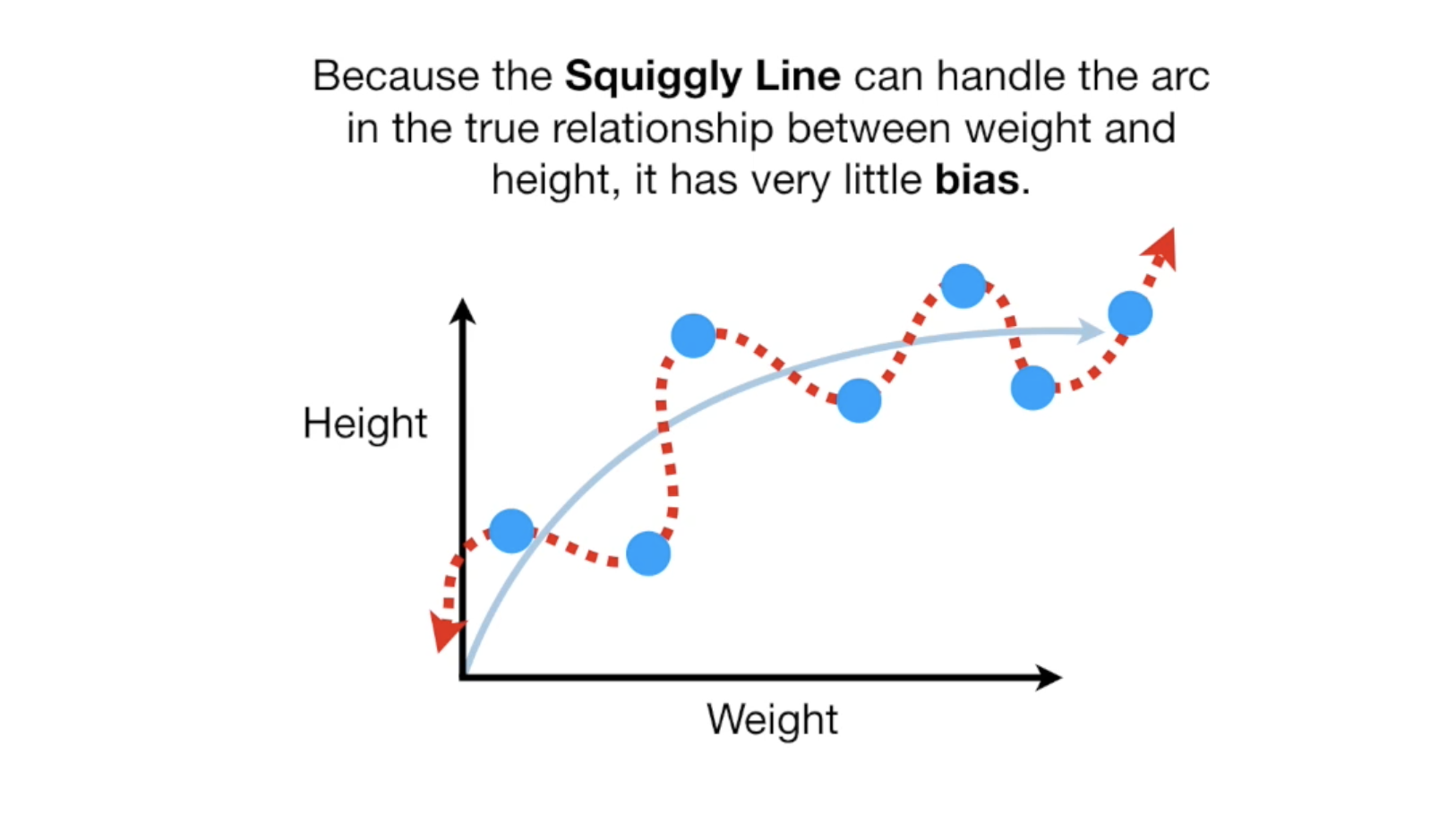
当我们用最小二乘法来衡量模型对测试数据的fit程度时,曲线模型无疑是最好的,但是基础,我们训练模型是用来做预测的,一个好的模型不是fit得好不好,而是预测的好不好。
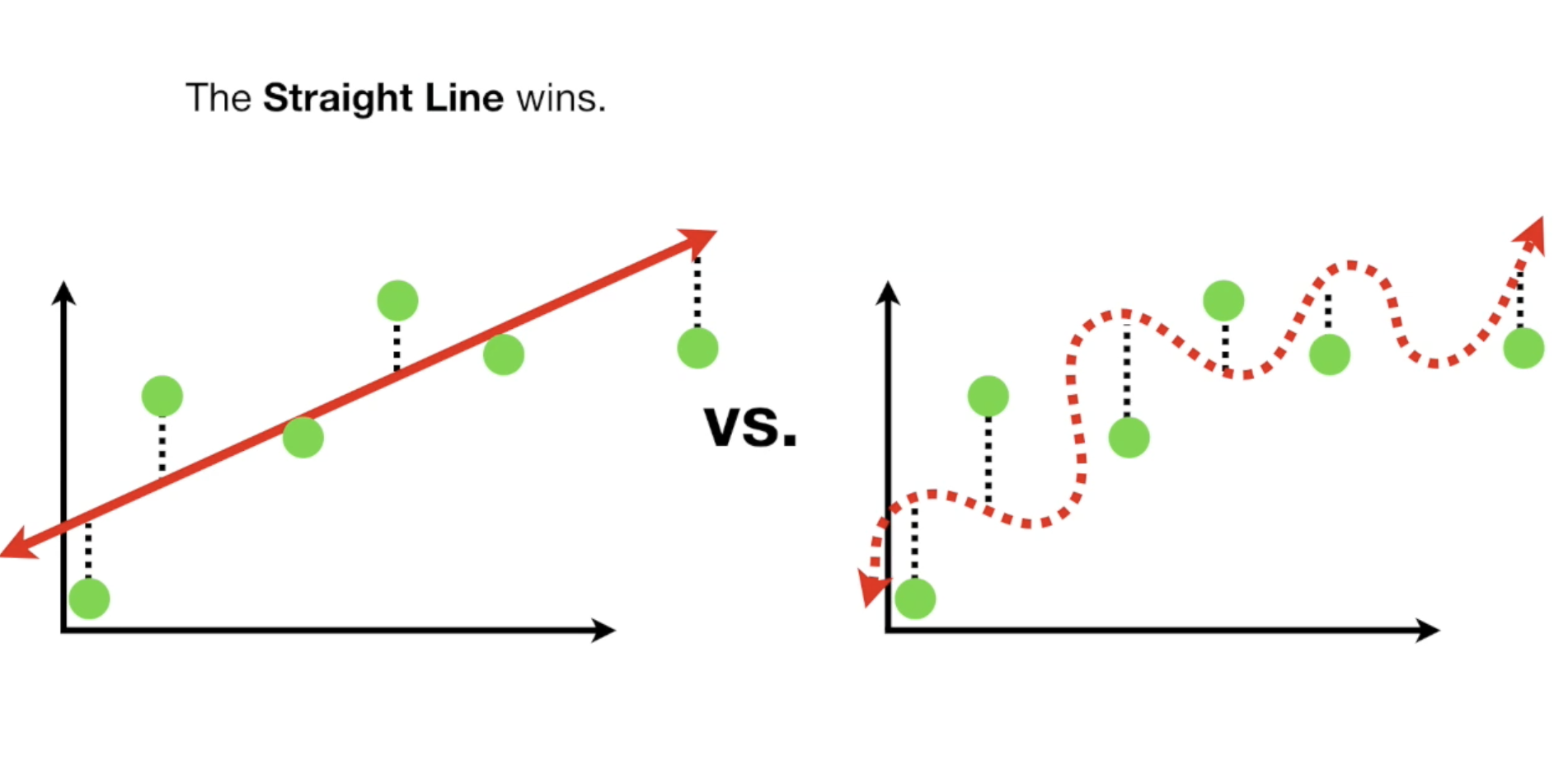
同样当我们用最小二乘法来测试预测结果时,LR直线模型却更好,这是因为曲线模型的Variance太高了。
bias高,可以理解为反应慢,但很稳。而Variance高,则意味反应很灵敏,发挥可能有时候很好,有时候很差。
直线的Variance比较低,因为对于不同的数据集的预测结果,算出来的最小二乘法之和比较低。
另外一种机器学习的描述方式,虽然我们的曲线模型对与训练数据fit的非常完美,但是在测试数据中却不理想,我们说这个模型overfit了。
理想的模型是variance和bias都比较低,能准确的反映数据的分布关系,以及做出稳定的预测。
要找到这个值,需要我们对模型做出调整,通常有三种方法:
- regularization
- boosting
- bagging
后续我们再来介绍这些概念。
ROC 与 AUC
ROC
还是这组老鼠的数据,根据它们的体总来判定它是否是肥胖症,蓝色的点是判断为肥胖症的老鼠,红色的则没有肥胖症,其中有一个红点很特殊,它看起来体重很高但是没有肥胖(这肯定是只肌肉鼠),同时数据中也有一些不是很重但患有肥胖症的,这是因为它很短小,却很胖。
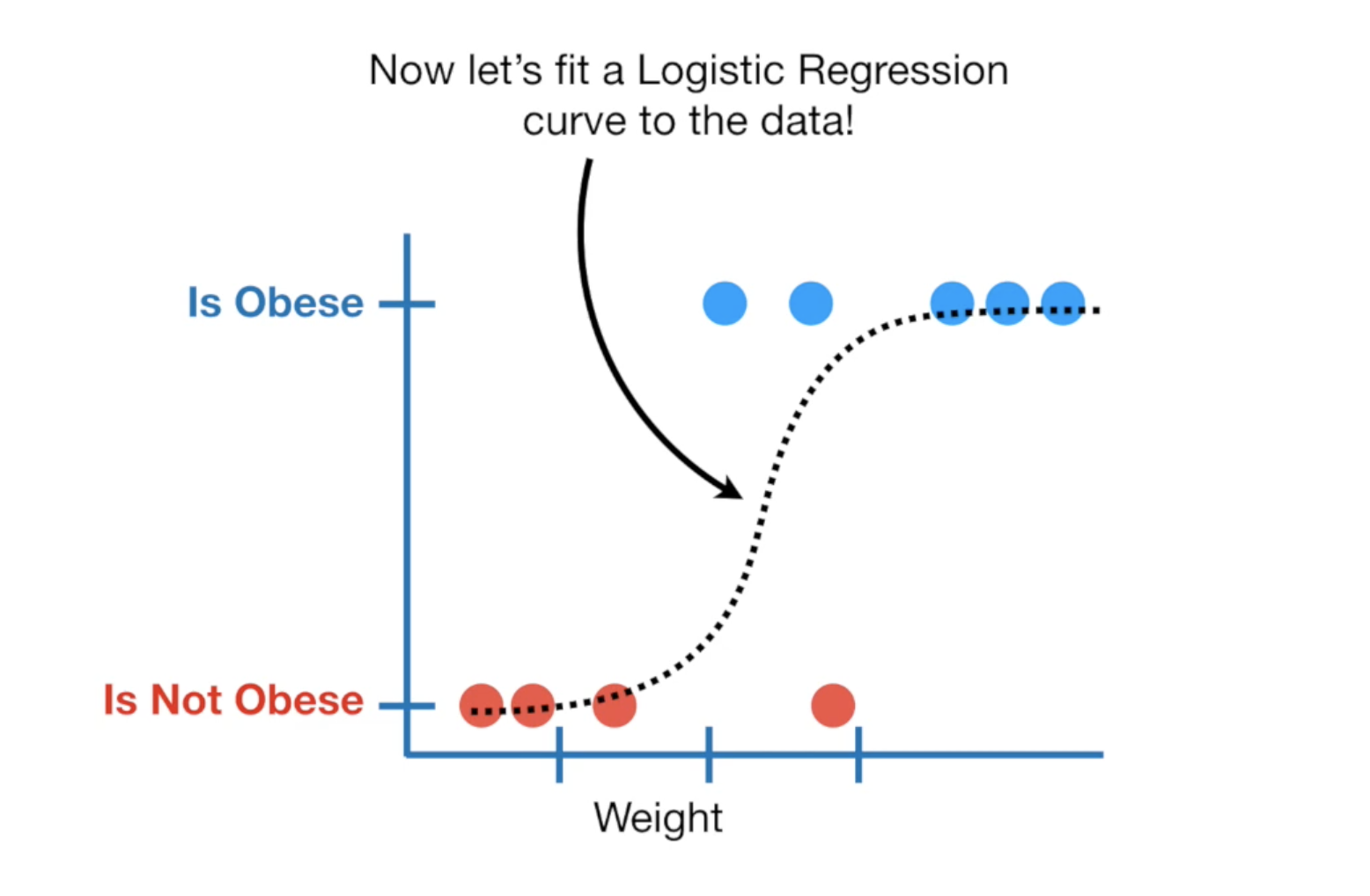
我们用LR fit这组数据,会得到这样的一个曲线,在LR中,y轴是我们的概率,值域为0-1,当你的LR模型绘制出来了的时候,给我一个老鼠的体重,我大概就可以判断它是不是有肥胖症,但是这需要一个threshold(临界值)作为判断点,比如在这里我们取概率为0.5对应的体重值。
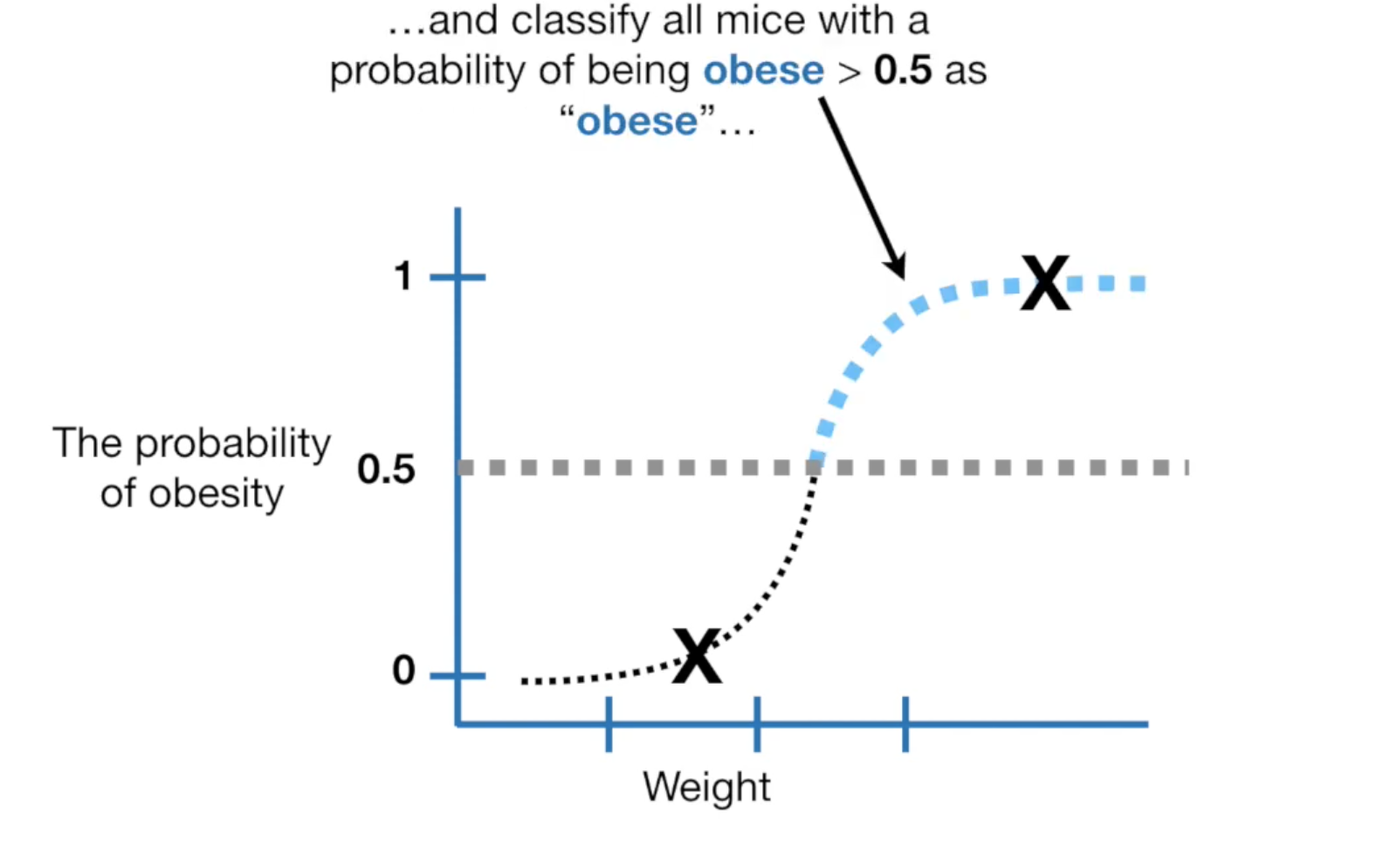
当你将这个threshold定位0.5,我们就可以用test数据统计confusion matrax,并计算Sensitivity 与 Specificity,如果你觉得threshold设为0.5不太合适,你可以将其设为0.6,然后再计算Sensitivity 与 Specificity对比看看。
这个threshold可以不断的做出调整,以适应(fit)我们的数据。
比如,我们设置为它为0.1。
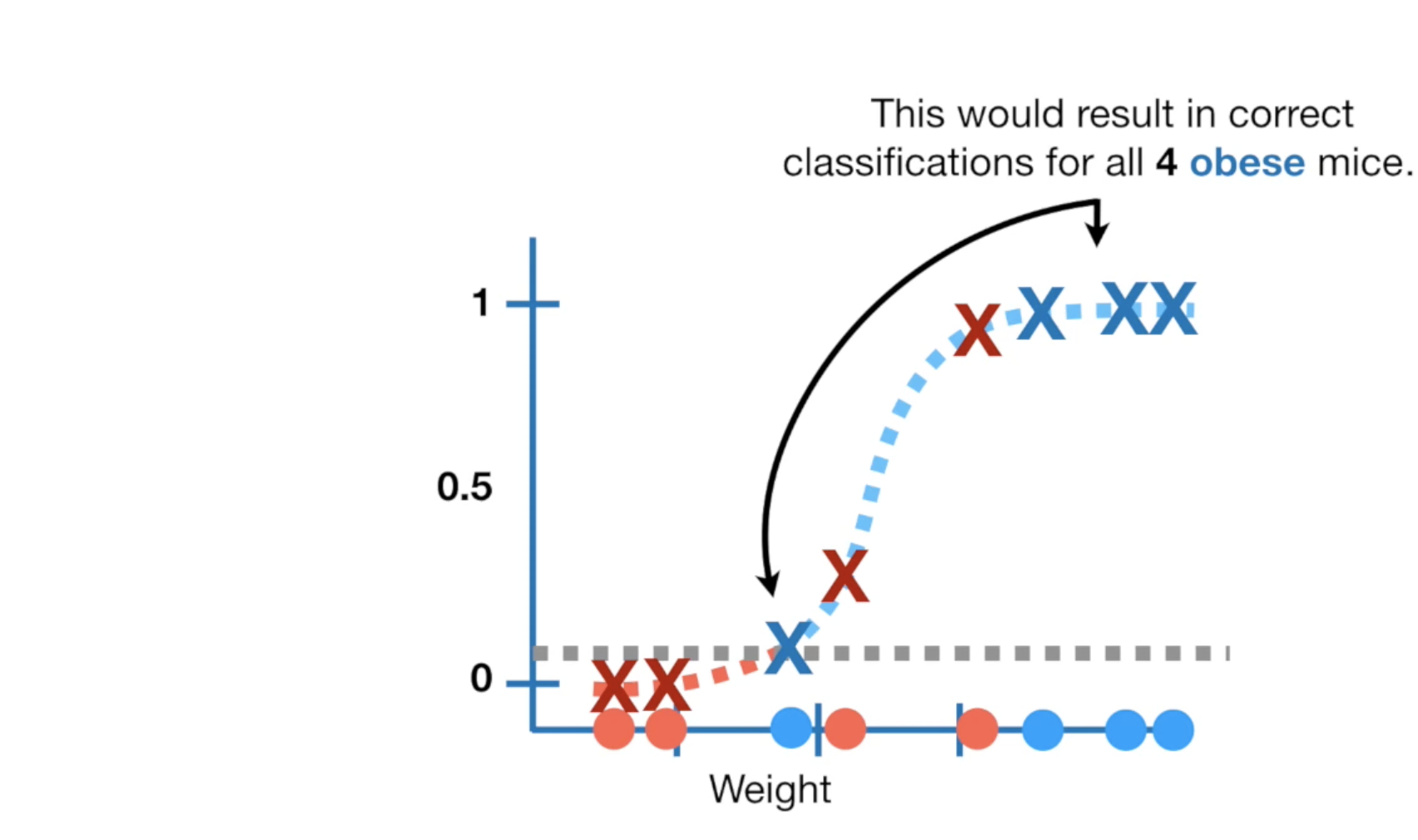
在这种情况下,所有0.1以上的都被标记成肥胖,增加了对肥胖预测的准确率,但会有一些非肥胖症的老鼠被预测称肥胖症。
你也可以设为0.9,所有0.9以下的老鼠都标记成非肥胖,这样会增加那些对非肥胖症预测的准确率,但会有一些肥胖的老鼠也被预测称非肥胖。
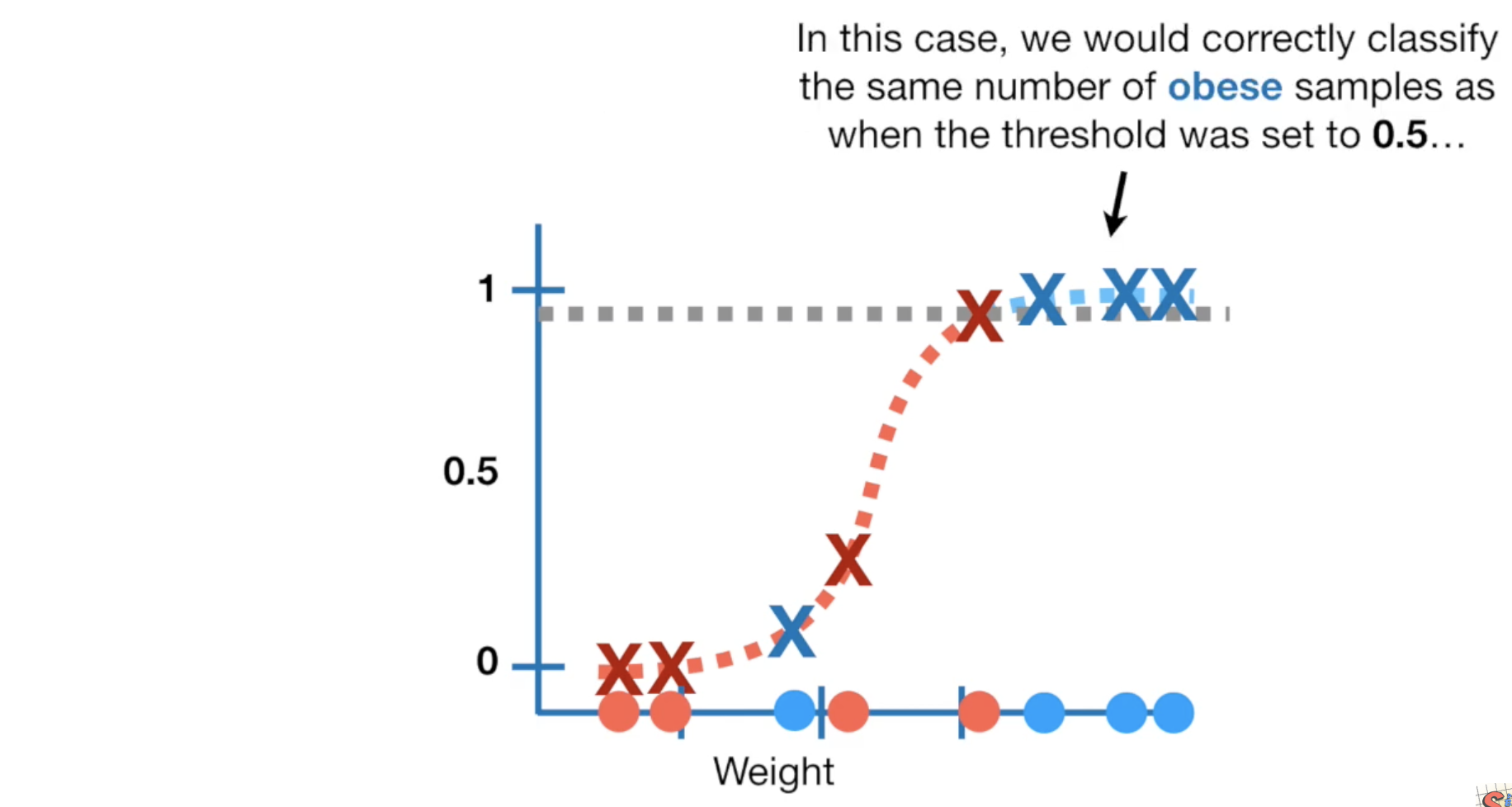
threshold可能是这其中的任何一个点,我们到底选哪个比较好呢?
这时候我们就可以使用ROC图像了,ROC图中x轴为 Specificity,y轴为Sensitivity,我们开始画图,第一步我们假设所有的老鼠都有肥胖症:

对于Sensitivity,我们计算后为1,它是所有真实肥胖症老鼠中有多少预测对了。这意味着所有的老鼠都标记为肥胖症,也就是说所有真实患有肥胖症的老鼠都预测成功了。
对于Specificity,计算后也为1,它是所有真实没有肥胖症的老鼠中,多少预测对了。这意味着所有不是肥胖症的老鼠都被标记为肥胖症了。
我们可以将这个点与0连线,在这条线上,Sensitivity和Specificity相等,这意味着我们对测试数据预测正确的值与预测错误的比例相等(那还不如靠猜)。
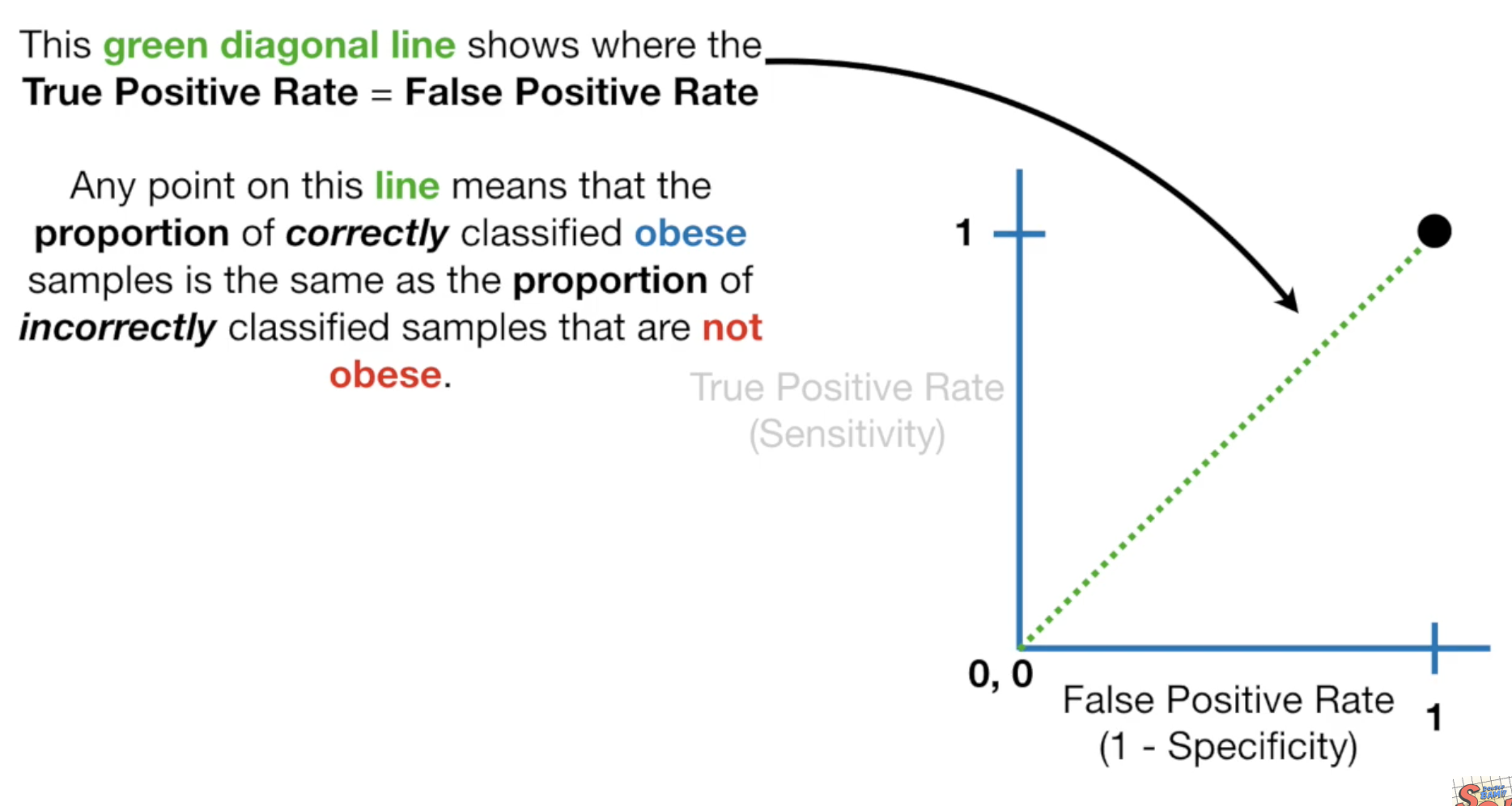
现在我们把threshold设为0.3,我们得到sensitivity为1,specificity为0.75.
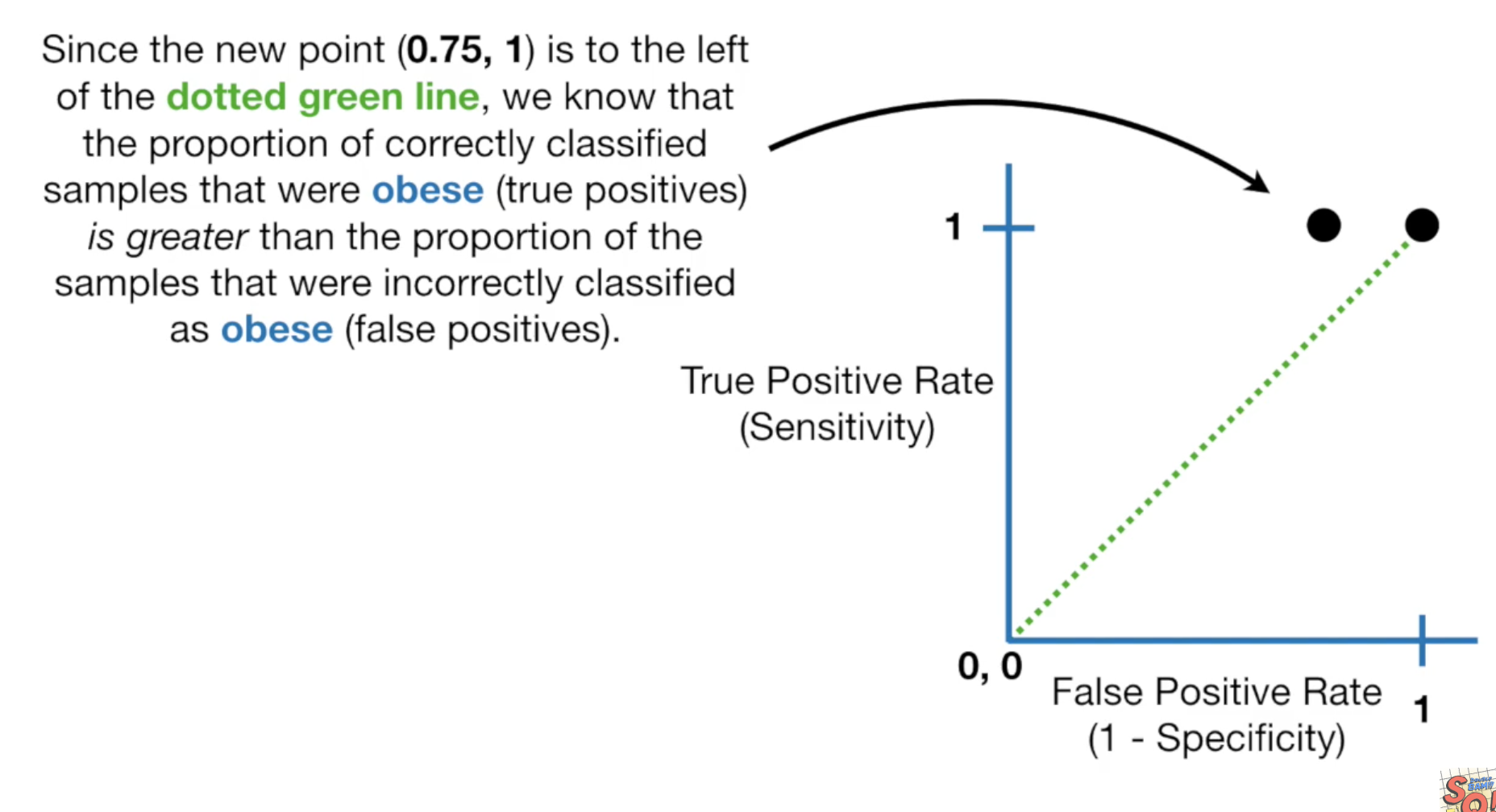
它的sensitivity>specificity,所以在图上它出现在绿虚线的左边,所以threshold为0.3比之前的值要好。
我们继续增加threshold

这个结果又要好一点,我们一直继续,直到我们把所有的老鼠都预测为非肥胖症,将所有的点连起来,这就是我们的ROC曲线了。
- y轴为:真实数据中,肥胖的预测正确了多少。
- x轴为:真实数据中,非肥胖的预测正确了多少。
- x轴也可能为:预测数据中,肥胖的预测正确了多少。
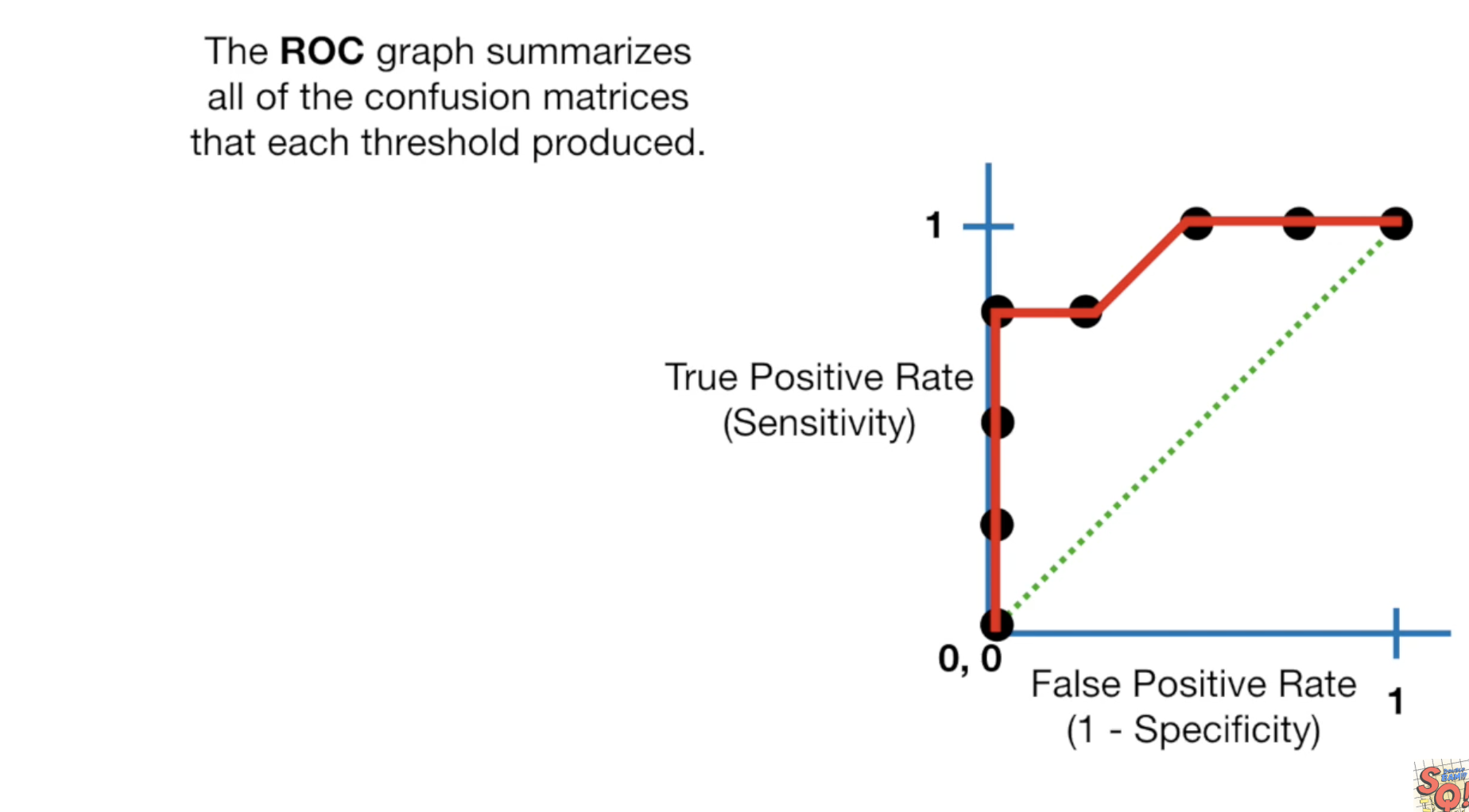
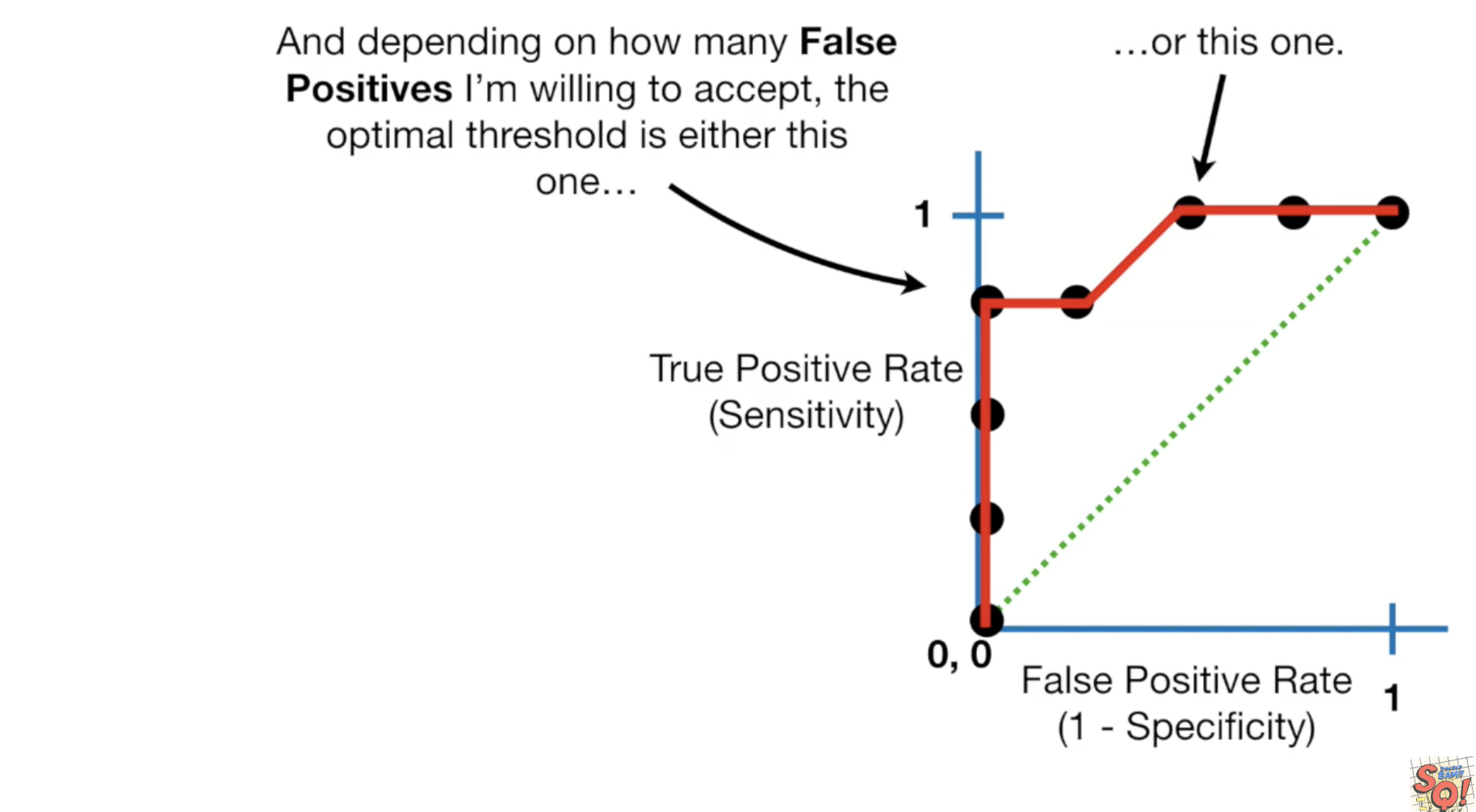
这个图中越靠近左上的点,结果越好。同时我们可以根据我们可以接受多大的错误率,来选择threshold,
AUC
AUC就是ROC下面的曲线,如果我们通过更换模型,让曲线下方的面积变大了,那么新模型就比原来的模型更好。
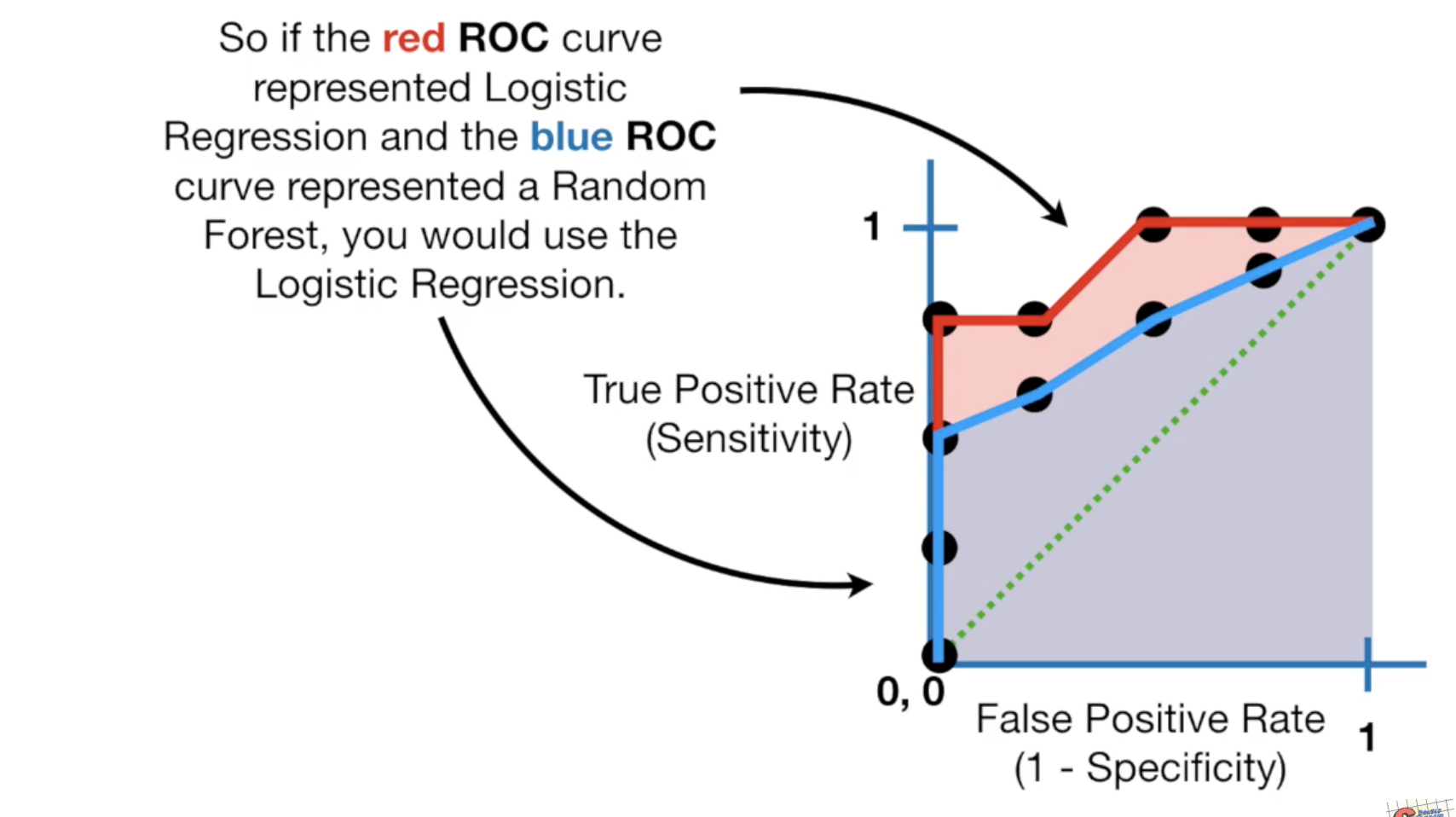
如果图中蓝色部分是随机森林模型生成的AUC,红色部分是LR生成的,那么你应该选择LR作为你的模型。
注:有时候人们会用precision代替specificity, 即precision=True Positive / True Positive + False positive
对比它们的定义:
specificity: 所有有肥胖症的老鼠中,预测正确了多少。 precision:所有预测为肥胖症的老鼠中,预测正确了多少。
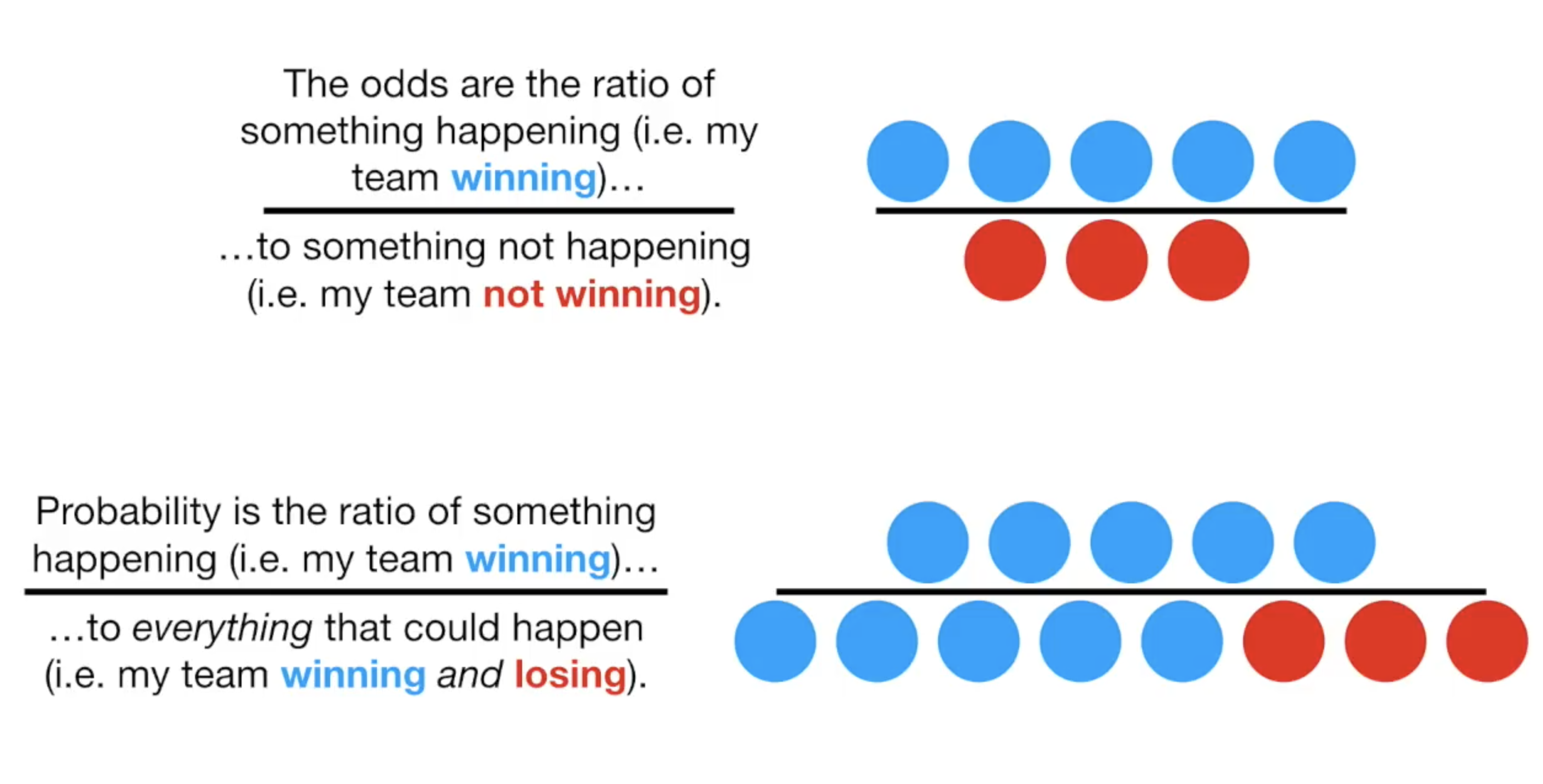
Odds 与 Probability
odds是你想要的结果除以你不想要的结果,而Probability是你想要的结果除以所有的结果。如在比赛中,你赢了5次,输了3次,那odds就是5/3,而概率测试5/8.
odds是可以通过概率来计算得出的,它的公式是:
\[\frac{p}{1-p}\]
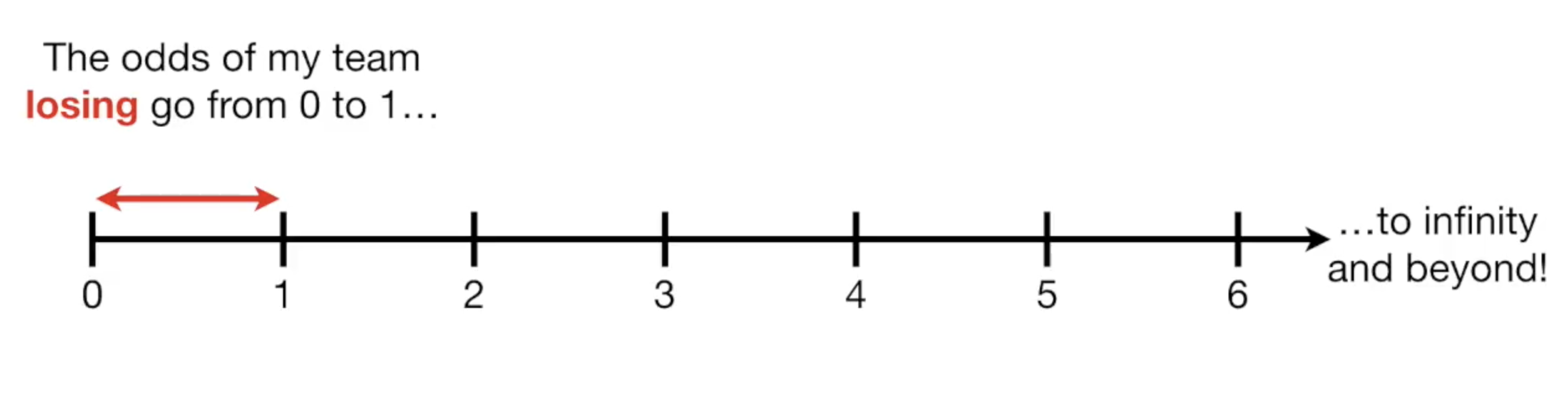
我们可以思考一下odds的取值范围,如果有一场比赛,因为我的实力很差,10次比赛输了8次,那么我的odds就是2/8,如果更糟,0/10,也就是0。
可见odds的值域中,最低值是0,从1-0是你所有输掉比赛的情况,而从1到无穷大则是你赢了比赛的情况,因为你赢了一万场输一场的情况也是有可能的,它的odds值为10000/1=10000。
把odds的值放到数轴上看,你会发现这样的一条线:
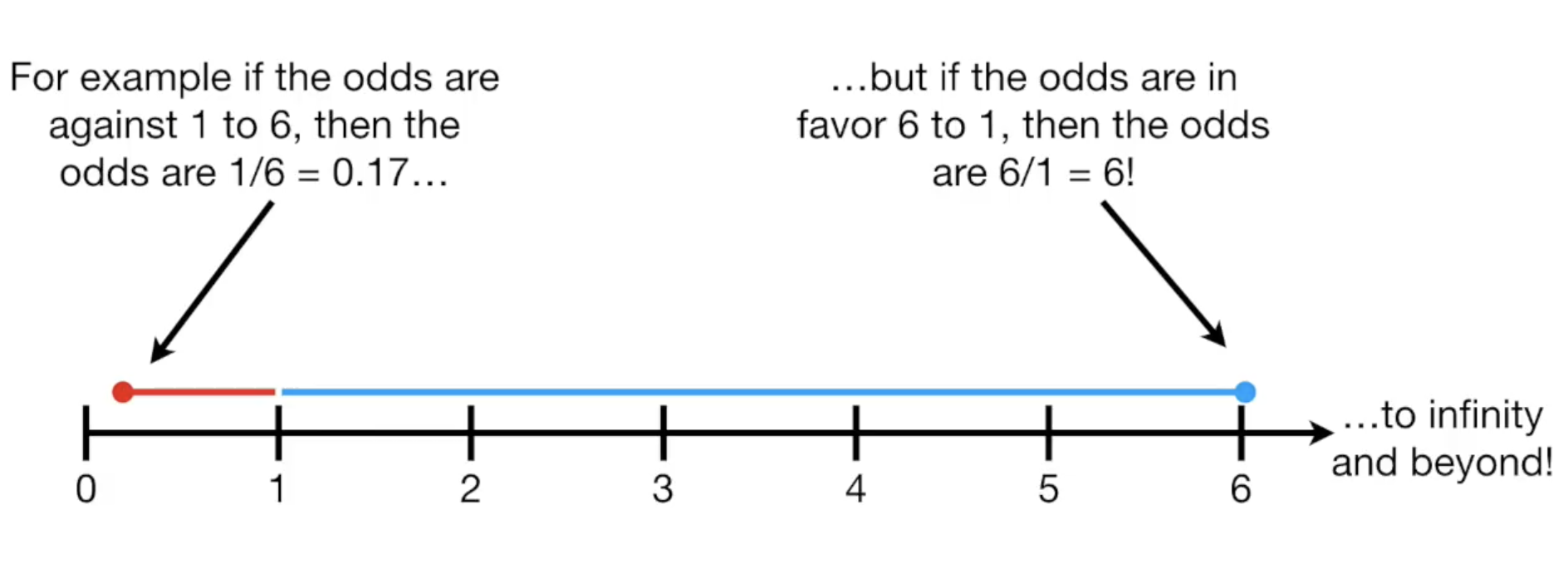
但这里存在一个小问题,比如对于1:6和6:1,我输了6场和赢了6场,这两个结果看起来是对成的,得到的值画在数轴上却是不对称的。
而使用log函数则可以解决这个问题:
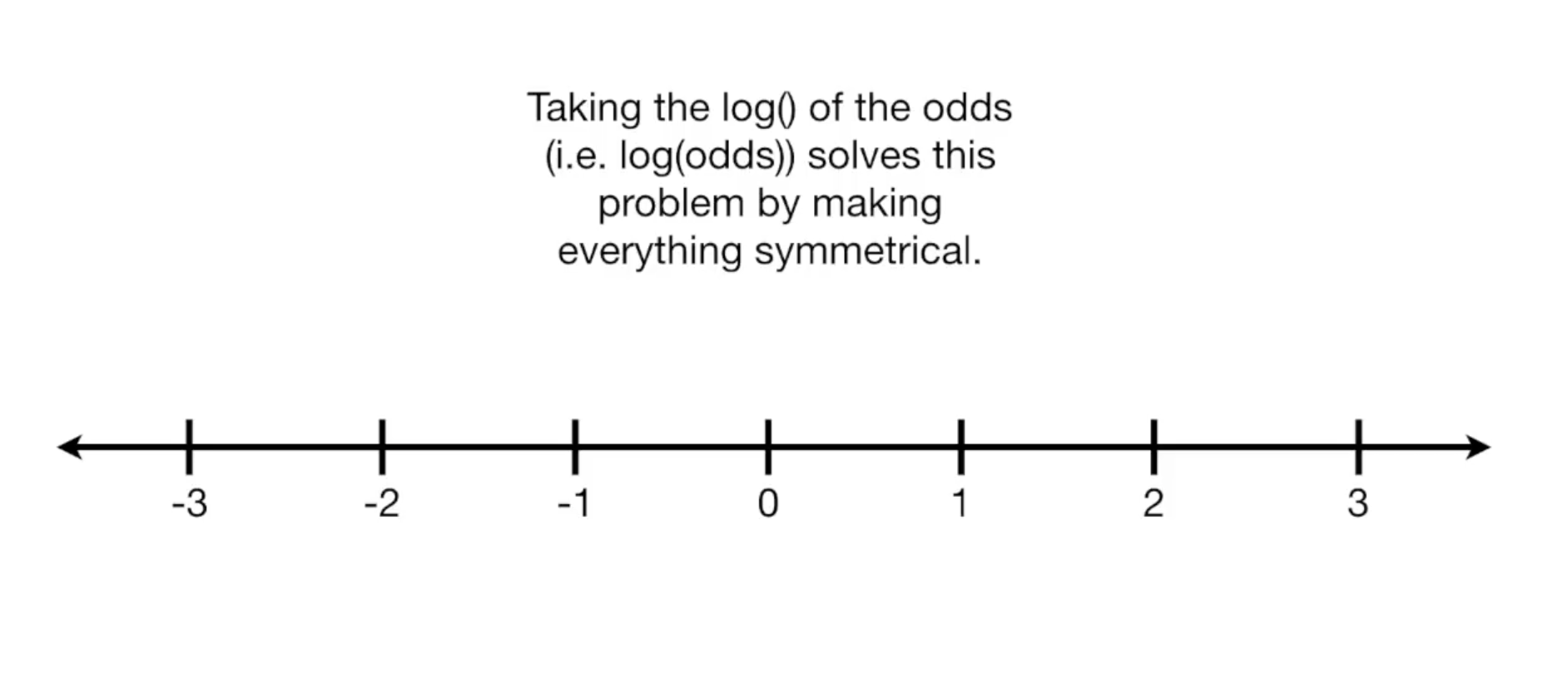
Odds Ratios 与 Log(Odds Ratios)
odds本质上是ratio,但odds≠odds ratio,我们说odds ratio,指的是odds之间的运算,也就是两个不同结果之间odds值的运算。
odds ratio算出来的值可能在0-1之间,也可能在1到无穷大之间,如果我们需要让odds ratio值数轴上显示,对它取对数会比较好。
我们来举个例子,下面是癌症与基因突变的一组数据:
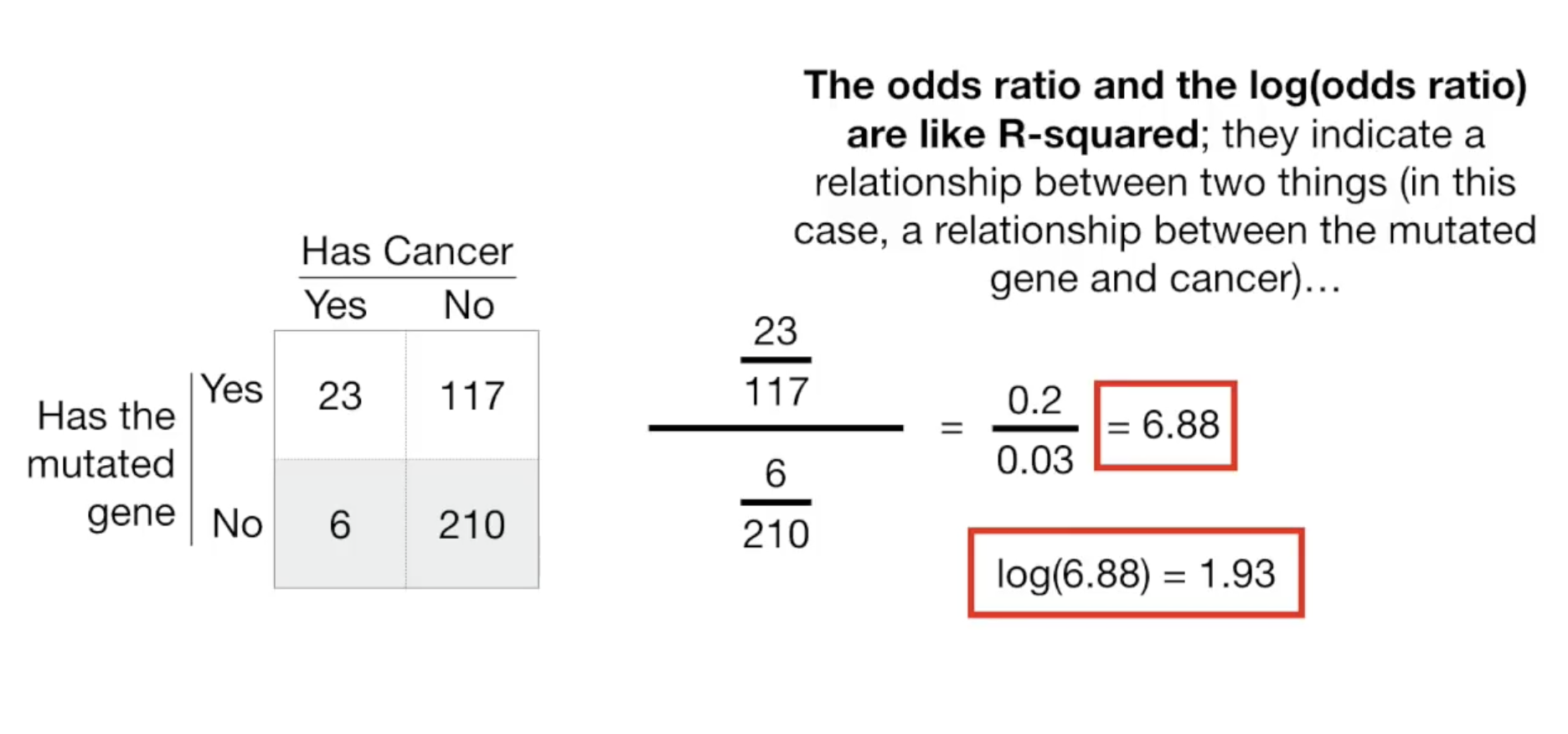
这是什么意思呢? odds ratio和log(ratio)说明了两个事物(这里是癌症与基因突变)之间的关系。
odds ratio值越大,基因突变这个变量对于预测癌症就越好用,越小,则说明这个变量不适合用来预测癌症。
然而要证明相关,还需要证明它们之间存在统计显著性,主要有三种方法:
- Fisher's Exact Test
- Chi-Square Test
- The Wald Test
有人比较喜欢用Fisher's Exact Test和Chi-Square Test计算P-Value,有人比较喜欢用The Wald Test计算P-Value和置信区间。
假设有如下表:
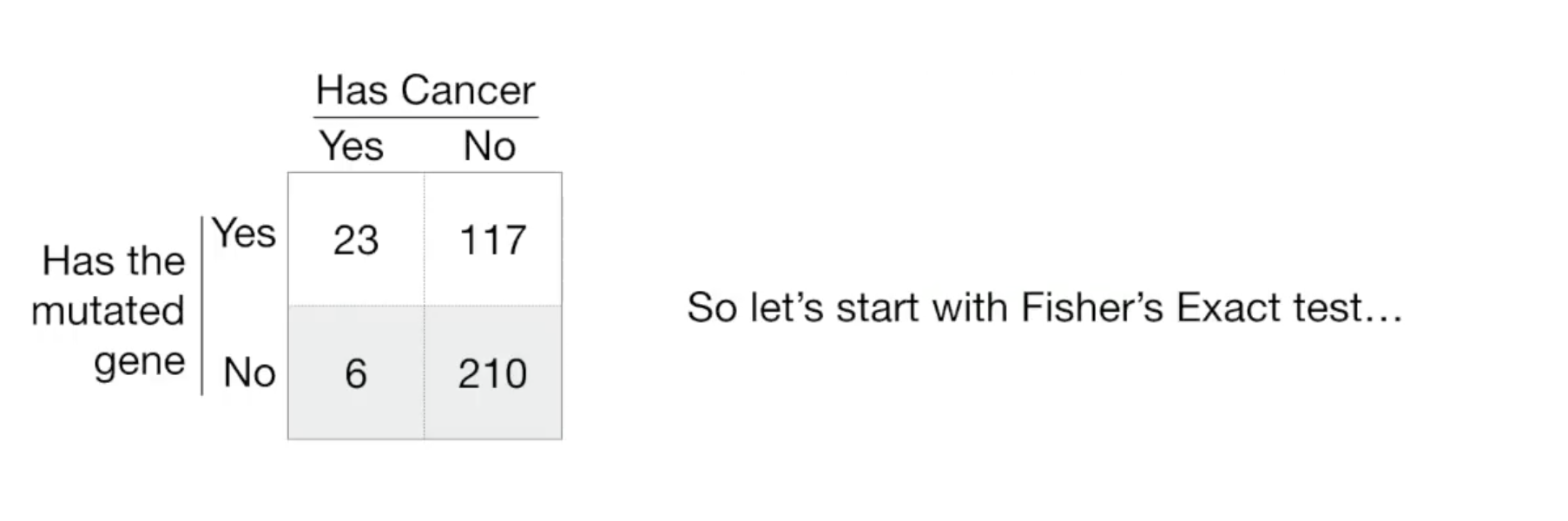
Fisher's Exact Test
Chi-Square Test
这是一种先假设癌症与基因变异之间没有关系的方法。 首先算出正常人患癌症的概率为:29/356 = 0.08.
有基因突变的为140人,如果按照正常人患癌症的概率,那么有基因突变的人中应该是 140*0.08=11.2 人有癌症,剩下 140-11.2=128.8 人无癌症。
同样的对于没有基因突变的人,患癌症的人为 216*0.08 = 17.3, 剩下 216-17.3 = 198.7人无癌症。
最后对比两个表,就可以算出p-vlue,如果你不知道具体如何算,可以参考别的文章。

The Wald Test
todo.
